高中数学组合几何选择题

直线y＝x＋b与曲线y＝－x＋ln x相切，则b的值为(　　)

A．－2

B．1

C．－

D．－1

设f(x)在(a，b)内可导，则f′(x)<0是f(x)在(a，b)内单调递减的(　　)

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分也不必要条件

设a为实数，函数f(x)＝x³＋ax²＋(a－2)x的导数是f′(x)，且f′(x)是偶函数，则曲线y＝f(x)在原点处的切线方程为(　　)

A．y＝－2x	B．y＝3x
C．y＝－3x	D．y＝4x

函数f(x)＝2lnx＋x²－bx＋a(b>0，a∈R)在点(b，f(b))处的切线斜率的最小值是(  )

A．2

B．2

C．

D．1

过曲线y＝x³＋x－2上一点P₀处的切线平行于直线y＝4x，则点P₀的一个坐标是(　　)

A．(0，－2)

B．(1，1)

C．(1，4)

D．(－1，－4)

已知函数f(x)＝＋xln x，则曲线y＝f(x)在x＝1处的切线方程为(　　)

A．x－y－3＝0

B．x－y＋3＝0

C．x＋y－3＝0

D．x＋y＋3＝0

设函数的图象上的点处的切线的斜率为k，若，则函数的图象大致为（    ）

曲线在点处的切线方程为（    ）

A．	B．
C．	D．

曲线在点处的切线方程为

A．	B．
C．	D．

以下正确命题的个数为（  ）
①命题“存在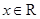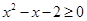，”的否定是：“不存在，”；
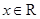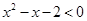②函数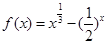的零点在区间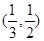内；
③ 函数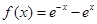的图象的切线的斜率的最大值是；
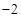④线性回归直线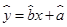恒过样本中心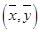，且至少过一个样本点.

A．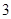

B．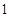

C．

D．

已知函数f(x)＝ax²＋3x－2在点(2，f(2))处的切线斜率为7，则实数a的值为(　　)

A．－1

B．1

C．±1

D．－2

设曲线y＝x^n＋1(n∈N^*)在点(1,1)处的切线与x轴的交点的横坐标为x_n，则x₁·x₂·…·x_n等于 (　　)．

A．

B．

C．

D．1

函数y＝xe^x在点(1，e)处的切线方程为(　　)．

A．y＝e^x	B．y＝x－1＋e
C．y＝－2ex＋3e	D．y＝2ex－e

已知函数f(x)＝x³－12x＋a，其中a≥16，则下列说法正确的是(　　)．

A．f(x)有且只有一个零点

B．f(x)至少有两个零点

C．f(x)最多有两个零点

D．f(x)一定有三个零点

已知函数的图象在处的切线斜率为
（），且当时，其图象经过，则（    ）

A．

B．

C．

D．