高中数学表面展开图试题

一个空间几何体的三视图及部分数据如图所示，则这个几何体的体积是 （   ）

A．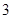

B．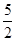

C．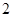

D．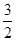

如图，长方体中，，点分别在上，，过点的平面与此长方体的面相交，交线围成一个正方形．
 
（1）在图中画出这个正方形（不必说明画法与理由）．
（2）求平面把该长方体分成的两部分体积的比值．

若圆锥的表面积是15π，侧面展开图的圆心角是60°，求圆锥的体积________________．

已知一个几何体的三视图如图所示，则该几何体的体积为

A．

B．

C．

D．

圆柱的轴截面是正方形，面积是，则它的侧面积是

A．

B．

C．

D．

正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积是

A．9

B．16

C．

D．

如图，一个空间几何体的正视图（或称主视图）、侧视图（或称左视图）、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为，那么这个几何体的体积为

A．1

B．

C．

D．

正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积是

A．9

B．16

C．

D．

如图，一个空间几何体的正视图（或称主视图）、侧视图（或称左视图）、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为，那么这个几何体的体积为

A．1

B．

C．

D．

一个长为，宽为，高为的密封的长方体盒子中放一个半径为的小球，无论怎样摇动盒子，则小球在盒子中总不能到达的空间的体积为             ．

某几何体的三视图如图所示，则该几何体的表面积为（  ）

A．

B．

C．

D．

如图，三棱柱中，侧棱垂直底面，是棱的中点．

（1）证明：平面⊥平面；
（2）平面分此棱柱为两部分，求这两部分体积的比．

棱长为2的正方体内切球的表面积为__________．

半径为的半圆卷成一个圆锥，则它的体积为（  ）

A．

B．

C．

D．

一个几何体的三视图如图所示，则该几何体的体积为（   ）

A．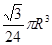

B．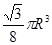

C．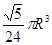

D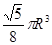．