如图,长方体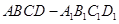 中,
中,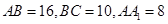 ,点
,点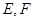 分别在
分别在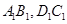 上,
上, ,过点
,过点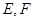 的平面
的平面 与此长方体的面相交,交线围成一个正方形.
与此长方体的面相交,交线围成一个正方形.

(1)在图中画出这个正方形(不必说明画法与理由).
(2)求平面 把该长方体分成的两部分体积的比值.
把该长方体分成的两部分体积的比值.
相关知识点
推荐套卷
如图,长方体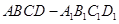 中,
中,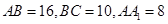 ,点
,点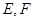 分别在
分别在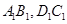 上,
上, ,过点
,过点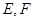 的平面
的平面 与此长方体的面相交,交线围成一个正方形.
与此长方体的面相交,交线围成一个正方形.

(1)在图中画出这个正方形(不必说明画法与理由).
(2)求平面 把该长方体分成的两部分体积的比值.
把该长方体分成的两部分体积的比值.