高中数学表面展开图选择题

平面四边形中，，，，将其沿对角线折成四面体，使平面平面，若四面体的顶点在同一个球面上，则该球的体积为 （）

A．

B．

C．

D．

平面四边形中，，，，将其沿对角线折成四面体，使平面平面，若四面体的顶点在同一个球面上，则该球的体积为（）

A．

B．

C．

D．

已知三棱锥的四个顶点均在半径为1的球面上，且满足，，，则三棱锥的侧面积的最大值为（）

A．

B．1

C．2

D．4

直角梯形，满足,现将其沿折叠成三棱锥，当三棱锥体积取最大值时其外接球的体积为（）

A．

B．

C．

D．

如图，网格纸上小正方形的边长为，粗实线画出的是某多面体的三视图，则该多面体的各面中，面积最大的是（）

A．

B．

C．

D．

如图，四棱锥中，底面是边长为2的正方形，其他四个侧面都是侧棱长为的等腰三角形，则二面角的大小（）

A．

B．

C．

D．

《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题："今有委米依垣内角，下周八尺，高五尺，问：积及为米几何？"其意思为："在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各为多少？"已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米有（ ）

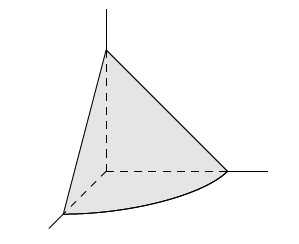
A．

14斛

B．

22斛

C．

36斛

D．

66斛

如果圆柱轴截面的周长为定值，则其体积的最大值为（）

A．p

B．p

C．p

D．p

某几何体的三视图如图所示，且该几何体的体积是，则正视图中的的值是（）

A．2

B．

C．

D．3

已知某四棱锥的三视图（单位：cm）如图所示，则该四棱锥的体积是 （）

A．	B．
C．	D．

—个几何体的三视图及其尺寸如图所示，则该几何体的表面积为（）

A．

B．

C．

D．

如图，过原点的直线与圆交于P、Q两点，点P在x轴上方，过点P、Q分别作x轴的垂线，垂足分别为点B、A，将x轴下方的图形沿x轴折起，使之与x轴上方的图形成直二面角，设点P的横坐标为x，三棱锥的体积记为，则函数的图象大致是（）

若三角形内切圆半径为，三边长分别为，则三角形的面积为，根据类比思想，若四面体内切球半径为，四个面的面积分别为，则这个四面体的体积为（）

A．

B．

C．

D．

三棱锥中，底面为等腰直角三角形，侧棱，二面角的余弦值为，则此三棱锥外接球的表面积为（）

A．

B．

C．

D．

如图，四面体中，，，，平面平面，若四面体的四个顶点在同一个球面上，则该球的体积为（）

A．

B．

C．

D．