高中数学表面展开图选择题

正三棱锥V-ABC的底面边长为，E,F,G,H分别是VA,VB,BC,AC的中点，则四边形EFGH的面积的取值范围是（）

A．	B．
C．	D．

将一张边长为6 cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形，将余下部分沿虚线折叠并拼成一个有底的正四棱锥（底面是正方形，顶点在底面的射影为正方形的中心）模型，如图2放置．若正四棱锥的正视图是正三角形（如图3），则正四棱锥的体积是（）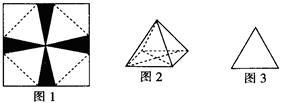

A．

B．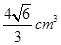

C．

D．

如图，在多面体中，已知是边长为1的正方形，且，均为正三角形，，，则多面体的体积为（）

A．

B．

C．

D．

一个棱锥的三视图如图（尺寸的长度单位为m），则该棱锥的全面积是( )（单位：m²）．

正视图侧视图俯视图

A．

B．

C．

D．

已知三棱锥，两两垂直且长度均为6，长为2的线段的一个端点在棱上运动，另一个端点在内运动（含边界），则的中点的轨迹与三棱锥的面所围成的几何体的体积为

A．	B．或
C．	D．或

已知三棱锥,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥的体积为,则球的表面积是（）

A．

B．

C．

D．

已知正三角形三个顶点都在半径为的球面上，球心到平面的距离为，点是线段的中点，过点作球的截面，则截面面积的最小值是（）

A．

B．

C．

D．

某几何体的三视图如图示，则此几何体的体积是（）

A．

B．

C．

D．

已知三棱锥的顶点A，B，C都在半径为2的球面上，O是球心，，当△与的面积之和最大时，三棱锥的体积为（）

A．

B．

C．

D．

已知某几何体的三视图如图所示，则该几何体的表面积等于（）

A．

B．160

C．

D．

如图，正方体的棱长为1，P为BC的中点，Q为线段上的动点，过
点A，P，Q的平面截该正方体所得的截面记为S．给出下列命题：

①当时，S为四边形；
②当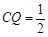时，S为等腰梯形；
③当时，S与C₁D₁的交点R满足；
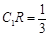④当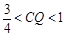时，S为六边形；
⑤当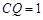时，S的面积为其中正确的是（）

A．①②③

B．①②③⑤

C．②③④⑤

D．①③④⑤

长方体的一个顶点上三条棱长为3、4、5，且它的八个顶点都在一个球面上，这个球的表面积是（）

A．20π

B．25π

C．50π

D．200π

已知某几何体的三视图如图所示，则该几何体的体积等于（）

A．	B．160
C．	D．60

若长方体中，，分别与底面所成的角为，，则长方体的外接球的体积为（）

A．

B．

C．

D．

三棱锥中，为等边三角形，，，三棱锥的外接球的表面积为（）

A．

B．

C．

D．