高中数学表面展开图选择题

将长、宽分别为4和3的长方形ABCD沿对角线AC折起，得到四面体A-BCD，则四面体A-BCD的外接球的体积为（）

A．

B．

C．

D．

已知三棱锥的四个顶点均在半径为1的球面上，且满足，，，则三棱锥的侧面积的最大值为（）

A．

B．1

C．2

D．4

如图所示是一几何体的三视图，正视图是一等腰直角三角形，且斜边BD长为2，侧视图是一直角三角形，俯视图为一直角梯形，且AB=BC=1，则异面直线PB与CD所成角的正切值是（）

A．1

B．

C．

D．

已知三棱锥,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥的体积为,则球的表面积是（）

A．

B．

C．

D．

一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积是（）

A．1

B．2

C．3

D．4

如图，网格纸上小正方形的边长为，粗实线画出的是某多面体的三视图，则该多面体的各面中，面积最大的是（）

A．

B．

C．

D．

如图，已知平面，、是上的两个点，、在平面内，且，，在平面上有一个动点，使得，则体积的最大值是（）

A．

B．

C．

D．

已知正三角形三个顶点都在半径为的球面上，球心到平面的距离为，点是线段的中点，过点作球的截面，则截面面积的最小值是（）

A．

B．

C．

D．

平行四边形ABCD中，·=0，沿BD将四边形折起成直二面角A一BD－C，
且，则三棱锥A－BCD的外接球的表面积为（　 　）

A．

B．

C．

D．

《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题："今有委米依垣内角，下周八尺，高五尺，问：积及为米几何？"其意思为："在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各为多少？"已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米有（ ）

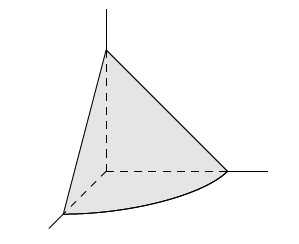
A．

14斛

B．

22斛

C．

36斛

D．

66斛

如图，正方体的棱长为1，P为BC的中点，Q为线段上的动点，过
点A，P，Q的平面截该正方体所得的截面记为S．给出下列命题：

①当时，S为四边形；
②当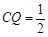时，S为等腰梯形；
③当时，S与C₁D₁的交点R满足；
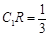④当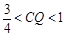时，S为六边形；
⑤当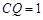时，S的面积为其中正确的是（）

A．①②③

B．①②③⑤

C．②③④⑤

D．①③④⑤

已知某几何体的三视图如图所示，则该几何体的体积等于（）

A．	B．160
C．	D．60

若长方体中，，分别与底面所成的角为，，则长方体的外接球的体积为（）

A．

B．

C．

D．

三棱锥中，为等边三角形，，，三棱锥的外接球的表面积为（）

A．

B．

C．

D．

某几何体的三视图如图所示，图中方格的长度为，则此几何体的体积为（）

A．

B．

C．

D．