高中数学表面展开图试题

如图，一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形，且直角边长为1，那么这个几何体的体积为（）

A．1

B．

C．

D．

如图，四棱锥中，底面，，底面为梯形，，，．

（1）求证：平面平面；
（2）求四棱锥的体积．

已知某几何体的三视图如图，其中正（主）视图中半圆的半径为1，则该几何体的体积为（）

A．24﹣

B．24﹣

C．24﹣π

D．24﹣

把正方形沿对角线折起，当以四点为顶点的三棱锥体积最大时，直线和平面所成的角的大小为（）度

A．90

B．60

C．45

D．30

把球的表面积扩大到原来的2倍，那么球的体积扩大到原来的（）

A．2倍

B．倍

C．倍

D．倍

四棱锥中，底面是边长为8的菱形，，若，平面平面.

（1）求四棱锥的体积；
（2）求证：．

如图所示是古希腊数学家阿基米德的墓碑文，墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等，相传这个图形表达了阿基米德最引以为自豪的发现．我们来重温这个伟大发现．圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为（）

A．，1

B．，1

C．，

D．，

如图是一个几何体的三视图，该几何体的体积是 ．

一个四棱锥的侧棱长都相等，底面是正方形，其主视图如图所示，该四棱锥侧面积等于（）

A．20	B．5
C．4（+1）	D．4

将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是（）

A．4π

B．3π

C．2π

D．π

一个几何体的三视图如图，则该几何体的体积是（）

A．+8

B．7+4

C．+8

D．+4

如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图，在直观图中，M是BD的中点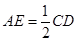，，侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示。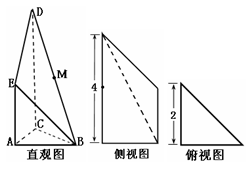

（Ⅰ）求出该几何体的体积；
（Ⅱ）试问在边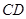上是否存在点N，使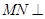平面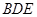？ 若存在，确定点N的位置(不需证明)；若不存在，请说明理由。

某几何体三视图如下，图中三个等腰三角形的直角边长都是，该几何体的体积为（）

A．	B．
C．	D．

正方体的棱长为，则其外接球的表面积为（）

A．

B．

C．

D．

设一个圆锥的侧面展开图是半径为的半圆，则此圆锥的体积为 ．