如图,已知直三棱柱ABC—A1B1C1,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为
| A.2:1 | B.3:1 | C.3:2 | D.4:3 |
三棱柱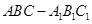 侧棱与底面垂直,体积为
侧棱与底面垂直,体积为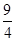 ,高为
,高为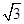 ,底面是正三角形,若
,底面是正三角形,若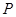 是
是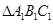 中心,则
中心,则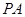 与平面
与平面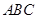 所成的角大小是( )
所成的角大小是( )
A.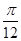 |
B.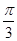 |
C.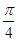 |
D.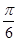 |
已知某几何体的三视图(单位: )如图所示,则该几何体的体积是( )
)如图所示,则该几何体的体积是( )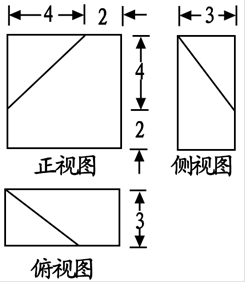
A.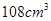 |
B.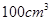 |
C.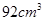 |
D.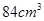 |
对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积 ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第 步,所得图形的面积
步,所得图形的面积 .若将以上操作类比推广到棱长为1的正方体中,到第n步,所得几何体的体积
.若将以上操作类比推广到棱长为1的正方体中,到第n步,所得几何体的体积 =____________.
=____________.
四面体ABCD的四个顶点都在球O的表面上,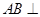 平面BCD,
平面BCD, 是边长为3的等边三角形.若
是边长为3的等边三角形.若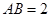 ,则球O的表面积为( )
,则球O的表面积为( )
A.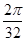 |
B.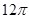 |
C. |
D. |