下列说法正确的是( )
| A.命题“∀x∈R,ex>0”的否定是“∃x∈R,ex>0” |
| B.命题“已知x、y∈R,若x+y≠3,则x≠2或y≠1”是真命题 |
| C.“x2+2x≥ax在x∈[1,2]上恒成立”⇔“(x2+2x)min≥(ax)max在x∈[1,2]上恒成立” |
| D.命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
给出下列结论:
①设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则α⊥β是a⊥b的必要不充分条件.
②在区间[-1,1]上随机取一个数x,则 的值介于0到
的值介于0到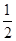 之间的概率为
之间的概率为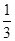
③从以正方体的顶点连线所成的直线中任取两条,则所取两条直线为异面直线的概率为
④将4个相同的红球和4个相同的篮球排成一排,从左到右每个球依次对应的序号为1,2,3,…,8,若同色球之间不加区分,则4个红球对应的序号之和小于4个蓝球对应的序号之和的排列方法种数为31.
其中正确结论的序号为 .
命题“若α= ,则tan α=1”的逆否命题是( )
,则tan α=1”的逆否命题是( )
A.若α≠ ,则tan α≠1 ,则tan α≠1 |
B.若α= ,则tan α≠1 ,则tan α≠1 |
C.若tan α≠1,则α≠ |
D.若tan α≠1,则α= |
己知命题p: 使得cos x≤x,则该命题的否定是( )
使得cos x≤x,则该命题的否定是( )
A. 使得cos x>x 使得cos x>x |
B. 使得cos x>x 使得cos x>x |
C. 使得cos x≥x 使得cos x≥x |
D. 使得cos x≤x 使得cos x≤x |
给出如下四个命题:
①若“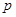 且
且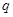 ”为假命题,则
”为假命题,则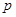 、
、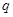 均为假命题;
均为假命题;
②命题“若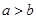 ,则
,则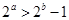 ”的否命题为“若
”的否命题为“若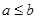 ,则
,则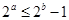 ”;
”;
③“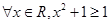 ”的否定是“
”的否定是“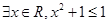 ”;
”;
④在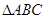 中,“
中,“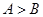 ”是“
”是“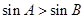 ”的充要条件.
”的充要条件.
其中不正确的命题的个数是( )
A.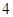 |
B.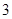 |
C.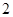 |
D.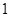 |
下列说法正确的是( )
A.“若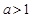 ,则 ,则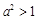 ”的否命题是“若 ”的否命题是“若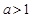 ,则 ,则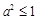 ” ” |
B.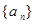 为等比数列,则“ 为等比数列,则“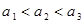 ”是“ ”是“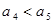 ”的既不充分也不必要条件 ”的既不充分也不必要条件 |
C.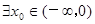 ,使 ,使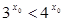 成立 成立 |
D.“若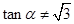 ,则 ,则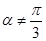 ”是真命题 ”是真命题 |
下列叙述正确的个数是( )
①若 为假命题,则
为假命题,则 均为假命题;
均为假命题;
②若命题 ,则
,则 ;
;
③在 中“
中“ ”是“
”是“ ”的充要条件;
”的充要条件;
④若向量 满足
满足 ,则
,则 与
与 的夹角为钝角。
的夹角为钝角。
| A.1 | B.2 | C.3 | D.4 |