设函数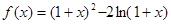
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设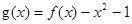 ,若关于x的方程
,若关于x的方程 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.
(3)证明不等式:
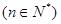
(本小题满分12分)将一张2×6米的硬钢板按图纸的要求进行操作:沿线裁去阴影部分,把剩余的部分按要求焊接成一个有盖的长方体水箱(⑦为底,①②③④为侧面,⑤+⑥为水箱盖,其中①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),设水箱的高为x米,容积为y立方米。
(1)写出y关于x的函数关系式;
(2)如何设计x的大小,使得水箱的容积最大?
已知函数 的定义域为
的定义域为 ,对定义域内的任意x,满足
,对定义域内的任意x,满足 ,当
,当 时,
时, (a为常),且
(a为常),且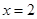 是函数
是函数 的一个极值点,
的一个极值点,
(1)求实数a的值;
(2)如果当 时,不等式
时,不等式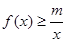 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(3)求证:
对于函数 ,若在定义域存在实数
,若在定义域存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数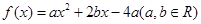 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设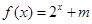 是定义在
是定义在 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
某商店以6元/千克的价格购进某种干果1140千克,并对其进行筛选分成甲级干果与乙级干果后同时开始销售。这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,且在同一天卖完;甲级干果从开始销售至销售的第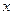 天的总销量
天的总销量 (千克)与
(千克)与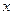 的关系为
的关系为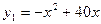 ;乙级干果从开始销售至销售的第
;乙级干果从开始销售至销售的第 天的总销量
天的总销量 (千克)与
(千克)与 的关系为
的关系为 ,且乙级干果的前三天的销售量的情况见下表:
,且乙级干果的前三天的销售量的情况见下表:
(1)求 、
、 的值;
的值;
(2)若甲级干果与乙级干果分别以8元/千克的6元/千克的零售价出售,则卖完这批干果获得的毛利润是多少元?
(3)问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克?
(说明:毛利润=销售总金额-进货总金额。这批干果进货至卖完的过程中的损耗忽略不计)