对于具有相同定义域 的函数
的函数 和
和 ,若存在
,若存在 ,使得
,使得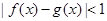 ,则
,则 和
和 在
在 上是“亲密函数”.给出定义域均为
上是“亲密函数”.给出定义域均为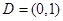 的四组函数如下:
的四组函数如下:
① ②
②
③ 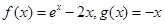 ④
④
其中,函数 和
和 在
在 上是“亲密函数”的是 .
上是“亲密函数”的是 .
已知函数 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的 ,都有f(x)
,都有f(x) 成立,求函数g(t)
成立,求函数g(t) 的最值
的最值
设函数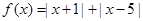 ,
,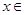
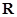 .
.
⑴ 求不等式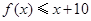 的解集;
的解集;
⑵ 如果关于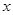 的不等式
的不等式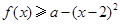 在
在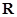 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
已知函数 ,g(x)=
,g(x)= ,a,b∈R.
,a,b∈R.
(1)求函数f(x)的单调区间;
(2)记函数h(x)=f(x)+g(x),当a=0时,h(x)在(0,1)上有且只有一个极值点,求实数b的取值范围;
(3)记函数F(x)=|f(x)|,证明:存在一条过原点的直线l与y=F(x)的图象有两个切点.
对于函数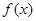 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数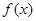 与
与 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
① ,
, ;
;
② ,
,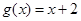 ;
;
③ ,
,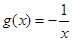 ;
;
④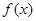
 ,
, ,
,
则在区间 上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( )
| A.①② | B.③④ | C.②③ | D.①④ |