安徽高考设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,则角C=( )
A.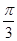 |
B. |
C.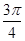 |
D.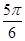 |
某航模兴趣小组的同学,为了测定在湖面上航模航行的速度,采用如下办法:在岸边设置两个观察点A、B ,且 AB长为80米,当航模在C处时,测得∠ABC=105°和∠BAC=30°,经过20 秒后,航模直线航行到 D 处,测得 ∠BAD=90°和 ∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)
右图是函数 在区间
在区间 上的图象。为了得到这个函数的图象,只要将
上的图象。为了得到这个函数的图象,只要将 的图象上所有的点( )
的图象上所有的点( )
A.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
B.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |