高中数学西姆松定理试题

已知函数，且函数的最小正周期为．
（1）求的单调递增区间；
（2）在△ABC中，角A，B，C所对的边分别是a，b，c，又，且△ABC的面积等于3，求边长a的值．

在△中，角的对边分别为，且满足．
（1）求的大小；
（2）若，求的值．

如图，在中，边上的中线长为3，且，．

（1）求的值；
（2）求边的长．

在中，三个内角所对的边为，若，，，则（     ）

A．

B．

C．4

D．

在平面四边形中， 。

（1）求的长；
（2）若，求的面积。

在△ABC中，角A、B、C所对的边分别为a、b、c，且满足cos，
（1）求△ABC的面积；
（2）若，求a的值．

在△ABC中，分别为角A、B、C的对边，若=（，），，且．
（Ⅰ）求角A的度数；
（Ⅱ）当，且△ABC的面积时，求边的值和△ABC的面积．

在△ABC中，a、b、c分别是角A、B、C的对边，且．
（Ⅰ）求角B的大小；
（Ⅱ）若，求△ABC的面积．

如图，某炮兵阵地位于A点，两观察所分别位于C，D两点．已知△ACD为正三角形，且DC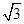＝km，当目标出现在B点时，测得∠BCD＝75°，∠CDB＝45°，求炮兵阵地与目标的距离．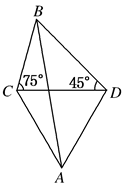

在△ABC中，BC＝a，AC＝b，a，b是方程的两个根，且．求：（1）角C的度数；  （2）AB的长度．

在△ABC中，若a＝7，b＝8，cosC＝，求最大角的余弦值．

在锐角△ABC中，a，b，c分别为角A，B，C所对的边，又c＝，b＝4，且BC边上的高h＝2．

（1）求角C；           
（2）求边a的长

△ABC中，已知a＝，c＝3，B＝45°，则b＝          ．

有关正弦定理的叙述：
①正弦定理仅适用于锐角三角形；
②正弦定理不适用于直角三角形；
③正弦定理仅适用于钝角三角形；
④在给定三角形中，各边与它的对角的正弦的比为定值；
⑤在△ABC中，sinA：sinB：sinC＝a：b：c．
其中正确的个数是（    ）

A．1

B．2

C．3

D．4

在中，内角所对的边分别是．已知，边上的中线长为4．
（Ⅰ）若，求；
（Ⅱ）求面积的最大值．