高中数学多项式的插值公式解答题

设向量，，.（1）若，求的值；
（2）设函数，求的最大、最小值.

已知函数，若的最大值为1
(Ⅰ)求的值，并求的单调递增区间;
(Ⅱ)在中，角、、的对边、、,若，且，试判断三角形的形状.

已知函数（其中）的图象如图所示．

(1) 求函数的解析式；
(2) 设函数，且，求的单调区间．

已知函数的最大值为2.

（1）求的值及的最小正周期；
（2）在坐标纸上做出在上的图像．

已知函数的最大值为2.

（1）求的值及的最小正周期；
（2）在坐标纸上做出在上的图像．

已知函数为偶函数，周期为2.
(Ⅰ)求的解析式；
(Ⅱ)若的值.

已知函数，函数与函数图像关于轴对称.
（1）当时，求的值域及单调递减区间；
（2）若，求值.

设函数的最大值为，最小值为，其中．
（1）求、的值（用表示）；
（2）已知角的顶点与平面直角坐标系中的原点重合，始边与轴的正半轴重合，终边经过点．求的值．  

设函数的最大值为，最小值为，其中．
（1）求、的值（用表示）；
（2）已知角的顶点与平面直角坐标系中的原点重合，始边与轴的正半轴重合，终边经过点．求的值．

（1）设，求的值；
（2）已知，且，求的值．

（1）设，求的值；
（2）已知，且，求的值．

某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
①；
②；
③；
④；
⑤.
(1)从上述五个式子中选择一个,求出常数；
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.

某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.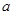
①；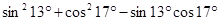
②；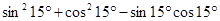
③；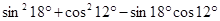
④；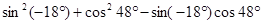
⑤.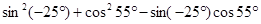
(1)从上述五个式子中选择一个,求出常数；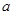
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.

已知点A（4，0）、B（0，4）、C（）
（1）若，且，求的大小；
（2），求的值．

在中，三个内角所对的边分别为，，的面积等于.
（1）求的值；
（2）求.