高中数学一阶、二阶线性常系数递归数列的通项公式选择题

在数列中，前项和为，，则当最小时，的值为（      ）

A．5

B．6

C．7

D．8

给出下列四个命题：
① 因为，所以；
② 由两边同除，可得；
③ 数列1，4，7，10，…，的一个通项公式是；
④ 演绎推理是由一般到特殊的推理，类比推理是由特殊到特殊的推理．
其中正确命题的个数有（     ）

A．1个

B．2个

C．3个

D．4个

在数列中，已知等于的个位数，则的值是

A．2

B．4

C．6

D．8

数列{a_n}中,a₁=1,对所有的n≥2,都有a₁·a₂·a₃·…·a_n=n²,则a₃+a₅等于(　　)

A．

B．

C．

D．

已知数列{a_n}的通项公式是a_n=n²+kn+2，若对于n∈N^*，都有a_n+1＞a_n成立，则实数的取值范围（　　）

A．k＞0

B．k＞﹣1

C．k＞﹣2

D．k＞﹣3

若数列满足＝(n∈N^*，为常数)，则称数列为“调和数列”．已知正项数列为“调和数列”，且，则的最大值是 (　 　)

A．10

B．100

C．200

D．400

已知f(x)＝＋log₂，则f＋f＋…＋f的值为(　　)

A．1

B．2

C．2 013

D．2 014

已知数列满足，定义：使乘积为正整数的叫做“期盼数”，则在区间内所有的“期盼数”的和为

A．

B．

C．

D．

对于数列{a_n}，a₁=4，a_n+1=f（a_n）n=1，2…，则a₂₀₁₁等于（　　）

x	1	2	3	4	5
f（x）	5	4	3	1	2

 
A．2        B．3        C．4        D．5

数列{a_n}满足a_n+a_n+1=(n∈N^*),a₂=2,S_n是数列{a_n}的前n项和,则S₂₀₁₅为(　　)

A．502

B．504

C．

D．2015

数列的一个通项公式是（     ）

A．

B．

C．

D．

已知数列{a_n}满足a_n+2=a_n+1+a_n，若a₁=1，a₅=8，则a₃=（　　）

A．1

B．2

C．3

D．

对数列，若区间满足下列条件：
①；②，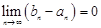
则称为区间套。下列选项中，可以构成区间套的数列是（     ）

A．；

B．

C．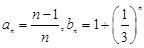

D．

已知数列{a_n}的前n项和S_n=n²-9n,第k项满足5<a_k<8,则k等于(　　)

A．9

B．8

C．7

D．6

已知数列的首项，且，则为 （    ）

A．7

B．15

C．30

D．31