.设集合 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列 的集合:
的集合:
① ②
②
 是与
是与 无关的常数.
无关的常数.
(Ⅰ)若 是等差数列,
是等差数列, 是其前n项的和,
是其前n项的和, ,证明:
,证明: ;
;
(Ⅱ)设数列 的通项为
的通项为 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设数列 的各项均为正整数,且
的各项均为正整数,且 ,试证
,试证 .
.
(本小题满分13分)已知数列 的前
的前 项和为
项和为 ,数列
,数列 满足
满足 ,
, .
.
(1)求数列 的通项公式; (2)求数列
的通项公式; (2)求数列 的前
的前 项和
项和 ;
;
(3)是否存在非零实数 ,使得数列
,使得数列 为等差数列,证明你的结论.
为等差数列,证明你的结论.
将石子摆成如图 的梯形形状.称数列
的梯形形状.称数列 为“梯形数”.根据图形的构成,数列第
为“梯形数”.根据图形的构成,数列第 项
项 ;第
;第 项
项 .
.
设数列{an}中,a1=2,an+1=an+n+1,则通项an= .
记等比数列 的前
的前 项积为
项积为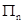 ,若
,若 ,则
,则 ( )
( )
| A.256 | B.81 | C.16 | D.1 |