若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2= .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
AB=|x1-x2|= =
= =
= =
= .
.
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0)、B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
函数f(x)=lnx+2x-1零点的个数为( )
| A.4 | B.3 | C.2 | D.1 |
将曲线C按伸缩变换公式 变换得曲线方程为
变换得曲线方程为 ,则曲线C的
,则曲线C的
方程为__________________。
若函数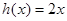 -
- +
+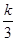 在(1,+
在(1,+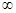 )是增函数,则实数k的取值范围是( )
)是增函数,则实数k的取值范围是( )
A.[-2,+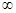 ) ) |
B.[2,+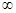 ) ) |
C.(-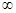 ,-2) ,-2) |
D.(-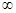 ,2] ,2] |
函数 是定义在R上的奇函数且
是定义在R上的奇函数且 也是奇函数,若
也是奇函数,若 ,则函数
,则函数 在区间
在区间 内的零点个数至少有
内的零点个数至少有
| A.4 | B.5 | C.6 | D.7 |