已知命题p:“∀x∈R,∃m∈R,使4x+2x·m+1=0”.若命题p为真命题,则实数m的取值范围是
| A.(-∞,-2] |
| B.[2,+∞) |
| C.(-∞,-2) |
| D.(2,+∞) |
下列有关命题的说法正确的是( )
A.若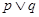 为真命题,则 为真命题,则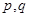 均为真命题 均为真命题 |
B.命题 “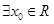 , ,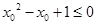 ”的否定是“ ”的否定是“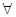  , ,  ” ” |
C.“ ”是“方程 ”是“方程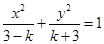 表示椭圆”的充要条件 表示椭圆”的充要条件 |
| D.“直线与双曲线有唯一交点”是“直线与双曲线相切”的必要不充分条件 |
命题“存在 R,
R,
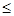 0”的否定是( ).
0”的否定是( ).
A.不存在 R, R,  >0 >0 |
B.存在 R, R,  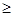 0 0 |
C.对任意的 R, R,  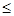 0 0 |
D.对任意的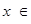 R, R,  >0 >0 |
命题“∃x∈R,ex<x”的否定是( )
| A.∃x∈R,ex>x | B.∀x∈R,ex≥x |
| C.∃x∈R,ex≥x | D.∀x∈R,ex>x |
命题“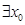 ∈N,x02 +2xo≥3”的否定为( )
∈N,x02 +2xo≥3”的否定为( )
A.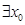 ∈N,x02 +2x0≤3 ∈N,x02 +2x0≤3 |
B.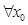 ∈N ,x2 +2x≤3 ∈N ,x2 +2x≤3 |
C.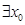 ∈N,x02 +2x0<3 ∈N,x02 +2x0<3 |
D.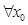 ∈N ,x2 +2x<3 ∈N ,x2 +2x<3 |
【原创】若命题“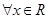 ,使
,使 ”是假命题,则实数
”是假命题,则实数 的取值范围为( )
的取值范围为( )
A. |
B.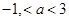 |
C.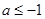 或 或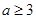 |
D.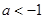 或 或 |
已知“命题p:∃x∈R,使得ax2+2x+1<0成立”为真命题,则实数a满足( )
| A.[0,1) | B.(-∞,1) |
| C.[1,+∞) | D.(-∞,1] |