高考名师推荐数学理科全称量词与存在性量词
已知命题p:“∀x∈[1,2],x2-a≥0”;命题q:“∃x∈R,x2+2ax+2-a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
| A.a≤-2或a=1 |
| B.a≤-2或1≤a≤2 |
| C.a≥1 |
| D.-2≤a≤1 |
来源:2014高考名师推荐数学理科全称量词与存在性量词
已知命题p:∃x∈[0,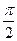 ],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
A.[-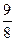 ,-1] ,-1] |
B.[-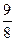 ,2] ,2] |
| C.[-1,2] |
D.[-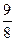 ,+∞) ,+∞) |
来源:2014高考名师推荐数学理科全称量词与存在性量词
已知命题p:“∀x∈R,∃m∈R,使4x+2x·m+1=0”.若命题p为真命题,则实数m的取值范围是
| A.(-∞,-2] |
| B.[2,+∞) |
| C.(-∞,-2) |
| D.(2,+∞) |
来源:2014高考名师推荐数学理科全称量词与存在性量词
已知命题p:m<0,命题q:∀x∈R,x2+mx+1>0成立,若“p∧q”为真命题,则实数m的取值范围是
| A.[-2,0] |
| B.(0,2) |
| C.(-2,0) |
| D.(-2,2) |
来源:2014高考名师推荐数学理科全称量词与存在性量词
已知命题p:∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)≥0,则¬p是( )
| A.∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0 |
| B.∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0 |
| C.∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0 |
| D.∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0 |
来源:2014高考名师推荐数学理科全称量词与存在性量词
已知命题p:∃x0∈R,使sin x0= ;命题q:∀x∈R,都有x2+x+1>0.
;命题q:∀x∈R,都有x2+x+1>0.
给出下列结论 ①命题“p∧q”是真命题; ②命题“¬p∨¬q”是假命题;
③命题“¬p∨q”是真命题; ④命题“p∨¬q”是假命题.
其中正确的是
| A.②③ |
| B.②④ |
| C.③④ |
| D.①②③ |
来源:2014高考名师推荐数学理科全称量词与存在性量词
已知命题p1:函数y=2x-2-x在R上为增函数,p2:函数y=2x+2-x在R上为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2和q4:p1∧(¬p2)中,真命题是
| A.q1,q3 |
| B.q2,q3 |
| C.q1,q4 |
| D.q2,q4 |
来源:2014高考名师推荐数学理科全称量词与存在性量词
 粤公网安备 44130202000953号
粤公网安备 44130202000953号