河北省承德市联校高二第一学期末理科数学卷
下列叙述错误的是( )
| A.频率是随机的,在试验前不能确定,随着试验次数的增加,频率越来越接近概率 |
B.若随机事件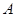 发生的概率为 发生的概率为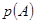 ,则 ,则 |
| C.互斥事件不一定是对立事件,但是对立事件一定是互斥事件 |
| D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性相同 |
两条曲线的方程分别是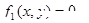 和
和 ,它们的交点是P(
,它们的交点是P(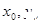 ),若曲线C的方程为
),若曲线C的方程为
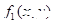 +
+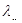
 ="0" (
="0" ( 、
、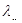 不全为0),则有( )
不全为0),则有( )
| A.曲线C恒经过点P | B.仅当 =0, =0,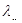  0时曲线C经过点P 0时曲线C经过点P |
C.仅当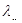 =0, =0,  0时曲线C经过点P 0时曲线C经过点P |
D.曲线C不经过点P |
从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加, 星期六有两人参加,星期日有一人参加,则不同的选派方法共有
| A.120种 | B.96种 | C.60种 | D.48种 |
命题“存在 R,
R,
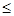 0”的否定是( ).
0”的否定是( ).
A.不存在 R, R,  >0 >0 |
B.存在 R, R,  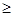 0 0 |
C.对任意的 R, R,  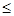 0 0 |
D.对任意的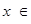 R, R,  >0 >0 |
在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连 续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
| A.甲地:总体均值为3,中位数为4 | B.乙地:总体均值为1,总体方差大于0 |
| C.丙地:中位数为2,众数为3 | D.丁地:总体均值为2,总体方差为3 |
下边程序框图可用来估计的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计的近似值为 ( )
| A.3.142 | B.3.142 | C.3.151 | D.3.152 |
在下列命题中:
①若向量 、
、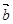 共线,则向量
共线,则向量 、
、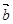 所在的直线平行;
所在的直线平行;
②若向量 、
、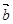 所在的直线为异面直线,则向量
所在的直线为异面直线,则向量 、
、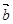 不共面;
不共面;
③若三个向量 、
、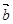 、
、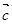 两两共面,则向量
两两共面,则向量 、
、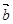 、
、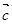 共面;
共面;
④已知空间不共面的三个向量 、
、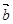 、
、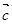 ,则对于空间的任意一个向量
,则对于空间的任意一个向量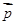 ,总存在实数
,总存在实数 、
、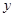 、
、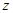 ,使得
,使得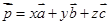 ;
;
其中正确的命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
已知x、y的取值如下表:
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析,y与x线性相关,且回归方程为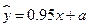 ,则
,则 .
.
已知 是
是 的充分条件而不是必要条件,
的充分条件而不是必要条件, 是
是 的必要条件,
的必要条件, 是
是 的充分条件,
的充分条件, 是
是 的必要条件.
的必要条件.
给出下列命题:
① 是
是 的充要条件;
的充要条件;
② 是
是 的充分条件而不是必要条件;
的充分条件而不是必要条件;
③ 是
是 的必要条件而不是充分条件;
的必要条件而不是充分条件;
④ 的必要条件而不是充分条件;
的必要条件而不是充分条件;
⑤ 是
是 的充分条件而不是必要条件;
的充分条件而不是必要条件;
其中正确命题的序号是 .
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列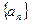 的前4项,后6组的频数从左到右依次是等差数列
的前4项,后6组的频数从左到右依次是等差数列 的前6项.
的前6项.
(Ⅰ)求等比数列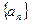 的通项公式;
的通项公式;
(Ⅱ)求等差数列 的通项公式;
的通项公式;
(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率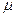 的大小.
的大小.
已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.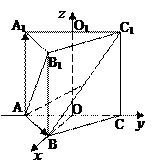
(Ⅰ)求正三棱柱的侧棱长.
(Ⅱ)若M为BC1的中点,试用基底向量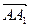 、
、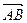 、
、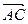 表示向量
表示向量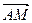 ;
;
(Ⅲ)求异面直线AB1与BC所成角的余弦值.
已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),……(x n,y n),…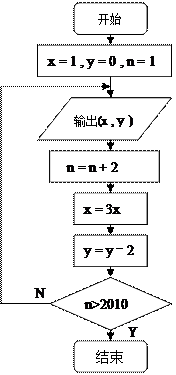
(Ⅰ)若程序运行中输出的一个数组是(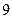 , t),则t =" " ;
, t),则t =" " ;
(Ⅱ)程序结束时,共输出(x , y )的组数为 ;
(Ⅲ)写出流程图的程序语句.
已知双曲线 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为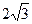 .过
.过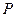
 的直线
的直线 与双曲线C交于不同的两点
与双曲线C交于不同的两点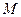 、
、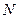 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)当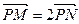 时,求直线
时,求直线 的方程;
的方程;
(Ⅲ)设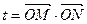 (
( 为坐标原点),求
为坐标原点),求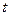 的取值范围.
的取值范围.
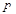 :
: ,条件
,条件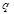 :
: ,且
,且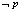 是
是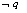 的充分不必要条件,则
的充分不必要条件,则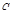 的取值范围是( )
的取值范围是( ) ;
; ;
;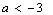 ;
; ;
; 与直线
与直线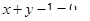 相交于
相交于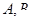 两点,过
两点,过 中点M与坐标原点的直线的斜率为
中点M与坐标原点的直线的斜率为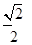 ,则
,则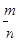 的值为( )
的值为( )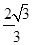
 与直线
与直线 +3有两个不同的公共点,则实数 k 的取值范围是( )
+3有两个不同的公共点,则实数 k 的取值范围是( )
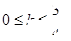
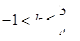

 上离点
上离点 最近的点恰好为顶点”成立的充要条件是( )
最近的点恰好为顶点”成立的充要条件是( )
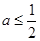

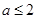
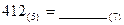
 上的点P到点(5,0)的距离为8.5,则点P到点(
上的点P到点(5,0)的距离为8.5,则点P到点(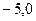 )的距离为______.
)的距离为______. 中,
中, .
.
 上任取一点
上任取一点 ,求使
,求使 的概率;
的概率; 内任作射线
内任作射线 ,求使
,求使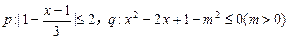 ;¬
;¬ 是¬
是¬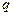 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号