期中备考总动员高三数学模拟卷【新课标1】9
【改编】已知0<a<2,复数 (i是虚数单位),则
(i是虚数单位),则 的取值范围是( )
的取值范围是( )
A. |
B.(1,5) | C.(1,3) | D. |
在 中,若
中,若 且
且 ,则该三角形的形状是( )
,则该三角形的形状是( )
| A.直角三角形 | B.钝角三角形 | C.等腰三角形 | D.等边三角形 |
在一次歌咏比赛中,七位裁判为以选手打出的分数如下:







去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
A. , , |
B. , , |
C. , , |
D. , , |
【改编】已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位: )可得这个几何体的表面积( )
)可得这个几何体的表面积( )

A. |
B. |
C. |
D.4 |
已知函数 (其中
(其中 ),其部分图像如下图所示,将
),其部分图像如下图所示,将 的图像纵坐标不变,横坐标变成原来的2倍,再向右平移1个单位得到
的图像纵坐标不变,横坐标变成原来的2倍,再向右平移1个单位得到 的图像,则函数
的图像,则函数 的解析式为( )
的解析式为( )

A. |
B. |
C. |
D. |
双曲线 的左、右焦点分别为
的左、右焦点分别为 ,渐近线分别为
,渐近线分别为 ,点
,点 在第一象限内且在
在第一象限内且在 上,若
上,若 ,
, ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A. |
B. |
C. |
D. |
已知抛物线 上一点
上一点 到其焦点的距离为
到其焦点的距离为 ,双曲线
,双曲线 的左顶点为
的左顶点为 ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线 平行,则正实数
平行,则正实数 的值为 。
的值为 。
在 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为______________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为______________________.
【改编】(本小题满分12分)等差数列 的前n项和为
的前n项和为 ,数列
,数列 是等比数列,满足
是等比数列,满足 ,
, ,
,  ,
, .
.
(Ⅰ)求数列 和
和 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本小题满分12分)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为 ,求
,求 .
.
(本小题满分12分)某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表1所示
表1
| |
参加社团活动 |
不参加社团活动 |
合计 |
| 学习积极性高 |
17 |
8 |
25 |
| 学习积极性一般 |
5 |
20 |
25 |
| 合计 |
22 |
28 |
50 |
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
 |
0.05 |
0.01 |
0.001 |
 |
3.841 |
6.635 |
10.828 |

【原创】(本小题满分12分)已知F1、F2是椭圆 的左右焦点,离心率为
的左右焦点,离心率为 ,D是上顶点,C是右顶点,△CDF2的面积为
,D是上顶点,C是右顶点,△CDF2的面积为 .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若动直线 与椭圆E相交于A、B求△AOB面积的最大值.
与椭圆E相交于A、B求△AOB面积的最大值.
(本小题满分12分)已知函数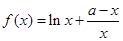 ,其中
,其中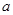 为常数,且
为常数,且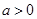 .
.
(Ⅰ)若曲线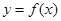 在点
在点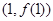 处的切线与直线
处的切线与直线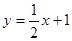 垂直,求
垂直,求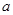 的值;
的值;
(Ⅱ)若函数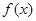 在区间
在区间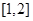 上的最小值为
上的最小值为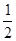 ,求
,求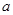 的值.
的值.
如图, 为直角三角形,
为直角三角形, ,以AB为直径的圆交AC于点E,点D是BC边的中点,连接OD交圆O于点M,求证:
,以AB为直径的圆交AC于点E,点D是BC边的中点,连接OD交圆O于点M,求证:
(Ⅰ)O、B、D、E四点共圆;
(Ⅱ) .
.
(原创)(本小题满分10分)选修4—4:坐标系与参数方程
已知极点与坐标原点重合,极轴与 轴非负半轴重合,
轴非负半轴重合, 是曲线
是曲线 :
: =
= 上任意一点,
上任意一点, =
= ,曲线
,曲线 与直线
与直线 :
: (
( 为参数)相交与
为参数)相交与 ,
, 两点,且|
两点,且| |=
|= .
.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
(Ⅱ)求实数 的值.
的值.
 ,
, ,
, , 则
, 则 ( )
( )



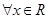 ,使
,使 ”是假命题,则实数
”是假命题,则实数 的取值范围为( )
的取值范围为( )
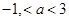
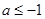 或
或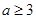
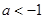 或
或
 ,
, ,则
,则 =( )
=( )



 ,
, 满足约束条件
满足约束条件 ,若
,若 的最小值为
的最小值为 ,则
,则 ( )
( )

 的图像大致为( )
的图像大致为( )
 有两个极值点
有两个极值点 ,
, ,且
,且 ,则( )
,则( )



 中,
中, ,
, ,
, ,若
,若 ,则
,则 .
. ,执行如图所示的程序框图,则输出的x不小于103的概率是________.
,执行如图所示的程序框图,则输出的x不小于103的概率是________.
 .
.  时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号