高中数学随机思想的发展解答题

甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动，在本次海选中有合格和不合格两个等级．若海选合格记1分，海选不合格记0分．假设甲、乙、丙海选合格的概率分别为，他们海选合格与不合格是相互独立的．
（1）求在这次海选中，这三名音乐爱好者至少有一名海选合格的概率；
（2）记在这次海选中，甲、乙、丙三名音乐爱好者所得分之和为随机变量,求随机变量的分布列和数学期望．

为了解甲、乙两个快递公司的工作状况，假设同一个公司快递员的工作状况基本相同，现从甲、乙两公司各随机抽取一名快递员，并从两人某月（30天）的快递件数记录结果中随机抽取10天的数据，制表如下：

甲公司某员工A		乙公司某员工B
3	9	6	5	8	3	3	2	3	4	6	6	6	7	7
						0	1	4	4	2	2	2

每名快递员完成一件货物投递可获得的劳务费情况如下：
甲公司规定每件4.5元；乙公司规定每天35件以内（含35件）的部分每件4元，超出35件的部分每件7元.
（1）根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数；
（2）为了解乙公司员工B的每天所得劳务费的情况，从这10天中随机抽取1天，他所得的劳务费记为（单位：元），求的分布列和数学期望；
（3）根据表中数据估算两公司的每位员工在该月所得的劳务费.

某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．

(1)分别求第3，4，5组的频率；
(2)若该校决定在笔试成绩较高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，
(ⅰ)已知学生甲和学生乙的成绩均在第三组，求学生甲和学生乙恰有一人进入第二轮面试的概率；
(ⅱ)学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试，设第4组中有名学生被考官L面试，求的分布列和数学期望．

某电视台组织部分记者，用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎，小数点后的一位数字为叶)：

（1）指出这组数据的众数和中位数；
（2）若幸福指数不低于9.5分，则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)任选3人，记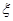表示抽到“极幸福”的人数，求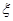的分布列及数学期望．

某单位从一所学校招收某类特殊人才．对位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试，其测试结果如下表：

例如，表中运动协调能力良好且逻辑思维能力一般的学生有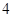人．由于部分数据丢失，只知道从这位参加测试的学生中随机抽取一位，抽到运动协调能力或逻辑思维能力优秀的学生的概率为．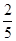
（1）求，的值；
（2）从参加测试的位学生中任意抽取位，求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率；
（3）从参加测试的位学生中任意抽取位，设运动协调能力或逻辑思维能力优秀的学生人数为，求随机变量的分布列及其数学期望．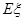

2014年2月21日，《中共中央关于全面深化改革若干重大问题的决定》明确：坚持计划生育的基本国策，启动实施一方是独生子女的夫妇可生育两个孩子的政策.为了解某地区城镇居民和农村居民对“单独两孩”的看法，某媒体在该地区选择了3600人调查，就是否赞成“单独两孩”的问题，调查统计的结果如下表：

	赞成	反对	无所谓
农村居民	2100人	120人	y人
城镇居民	600人	x人	z人

已知在全体样本中随机抽取1人，抽到持“反对”态度的人的概率为0.05.
（1）现在分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？
（2）在持“反对”态度的人中，用分层抽样的方法抽取6人，按每组3人分成两组进行深入交流，求第一组中农村居民人数的分布列和数学期望.

“蛟龙号”从海底中带回的某种生物，甲乙两个生物小组分别独立开展对该生物离开恒温箱的成活情况进行研究，每次试验一个生物，甲组能使生物成活的概率为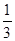，乙组能使生物成活的概率为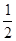，假定试验后生物成活，则称该试验成功，如果生物不成活，则称该次试验是失败的．
（1）甲小组做了三次试验，求至少两次试验成功的概率；
（2）如果乙小组成功了4次才停止试验，求乙小组第四次成功前共有三次失败，且恰有两次连续失败的概率；
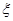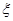（3）若甲乙两小组各进行2次试验，设试验成功的总次数为，求的期望．

近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重．大气污染可引起心悸．呼吸困难等心肺疾病．为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查得到了如下的列联表：

	患心肺疾病	不患心肺疾病	合计
男		5
女	10
合计			50

已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为．
（1）请将上面的列联表补充完整；
（2）是否有99.5%的把握认为患心肺疾病与性别有关？说明你的理由；
（3）已知在患心肺疾病的10位女性中，有3位又患胃病．现在从患心肺疾病的10位女性中，选出3名进行其他方面的排查，记选出患胃病的女性人数为，求的分布列，数学期望以及方差．下面的临界值表供参考：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式，其中）

生产A，B两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：

测试指标	[70,76)	[76,82)	[82,88)	[88,94)	[94,100]
元件A	8	12	40	32	8
元件B	7	18	40	29	6

（1）试分别估计元件A、元件B为正品的概率；
（2）生产一件元件A，若是正品可盈利50元，若是次品则亏损10元；生产一件元件B，若是正品可盈利100元，若是次品则亏损20元，在（1）的前提下：
（i）求生产5件元件B所获得的利润不少于300元的概率；
（ii）记X为生产1件元件A和1件元件B所得的总利润，求随机变量X的分布列和数学期望．

A、B两个投资项目的利润率分别为随机变量X₁和X₂，根据市场分析，X₁和X₂的分布列分别为

X1	5%	10%
P	0.8	0.2

 

X2	2%	8%	12%
P	0.2	0.5	0.3

(1)在A，B两个项目上各投资100万元，Y₁和Y₂分别表示投资项目A和B所获得的利润，求方差V(Y₁)、V(Y₂)；
(2)将x(0≤x≤100)万元投资A项目，100－x万元投资B项目，f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和．求f(x)的最小值，并指出x为何值时，f(x)取到最小值．

甲、乙两名射手各打了10发子弹，其中甲击中环数与次数如下表

环数	5	6	7	8	9	10
次数	1	1	1	1	2	4

乙射击的概率分布列如表

环数	7	8	9	10
概率	0.2	0.3	p	0.1

(1)若甲，乙两人各打一枪，求共击中18环的概率及p的值；
(2)比较甲，乙两人射击水平的优劣．

甲、乙两人各进行3次射击，甲每次击中目标的概率为，乙每次击中目标的概率为.
(1)求乙至多击中目标2次的概率；
(2)记甲击中目标的次数为Z，求Z的分布列、数学期望和标准差．

某地位于甲、乙两条河流的交汇处，根据统计资料预测，今年汛期甲河流发生洪水的概率为0.25，乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响)．现有一台大型设备正在该地工作，为了保护设备，施工部门提出以下三种方案：
方案1：运走设备，此时需花费4000元；
方案2：建一保护围墙，需花费1000元，但围墙只能抵御一个河流发生的洪水，当两河流同时发生洪水时，设备仍将受损，损失约56000元；
方案3：不采取措施，此时，当两河流都发生洪水时损失达60000元，只有一条河流发生洪水时，损失为10000元．
(1)试求方案3中损失费X(随机变量)的分布列；
(2)试比较哪一种方案好．

第16届亚运会于2010年11月12日在广州举办，运动会期间来自广州大学和中山大学的共计6名大学生志愿者将被随机平均分配到跳水、篮球、体操这三个比赛场馆服务，且跳水场馆至少有一名广州大学志愿者的概率是.
(1)求6名志愿者中来自广州大学、中山大学的各有几人？
(2)设随机变量X为在体操比赛场馆服务的广州大学志愿者的人数，求X的分布列及均值．

在高中“自选模块”考试中，某考场的每位同学都选了一道数学题，第一小组选《数学史与不等式选讲》的有1人，选《矩阵变换和坐标系与参数方程》的有5人，第二小组选《数学史与不等式选讲》的有2人，选《矩阵变换和坐标系与参数方程》的有4人，现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率；
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数，求X的分布列和数学期望．