投掷两个骰子，至少有一个4点或5点出现时，就说这次试验成功，则在10次试验中，成功次数X的期望是________．
设随机变量X～B(2，p)，Y～B(3，p)，若P(X≥1)＝
，则P(Y＝2)＝________.
甲、乙两人进行乒乓球比赛，采用“五局三胜制”，即五局中先胜三局为赢，若每场比赛甲获胜的概率是
，乙获胜的概率是
，则比赛以甲三胜一负而结束的概率为________．
某射手射击1次，击中目标的概率是0.9，他连续射击4次，且各次射击是否击中目标相互之间没有影响，有下列结论：①他第3次击中目标的概率是0.9；②他恰好击中目标3次的概率是0.93×0.1；③他至少击中目标1次的概率是1－0.14.其中结论正确的是________．(写出所有正确结论的序号)
已知一个射手每次击中目标的概率为p＝
，他在4次射击中，命中两次的概率为________，刚好在第二、第三两次击中目标的概率为________．
甲、乙两人各射击1次，击中目标的概率分别是
和
，假设两人射击目标是否击中相互之间没有影响，每人各次射击是否击中目标也没有影响．则两人各射击4次，甲恰好有2次击中目标且乙恰好有3次击中目标的概率为________．
在4次独立重复试验中事件A出现的概率相同，若事件A至少发生1次的概率为
，则事件A在1次试验中出现的概率为________．
已知随机变量X服从二项分布，X～B
，则P(X＝1)的值为________．
下面随机变量X的分布列不属于二项分布的是________．
①据中央电视台新闻联播报道，下周内在某网站下载一次数据，电脑被感染某种病毒的概率是0.65.设在这一周内，某电脑从该网站下载数据n次中被感染这种病毒的次数为X；②某射手射击击中目标的概率为p，设每次射击是相互独立的，从开始射击到击中目标所需要的射击次数为X；③某射手射击击中目标的概率为p，设每次射击是相互独立的，射击n次命中目标的次数为X；④位于某汽车站附近有一个加油站，汽车每次出站后到这个加油站加油的概率为0.6，国庆节这一天有50辆汽车开出该站，假设一天里汽车去该加油站加油是相互独立的，去该加油站加油的汽车数为X.
某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮．假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了4个问题就晋级下一轮的概率等于________．
有20个零件，其中16个一等品，4个二等品，若从这20个零件中任意取3个，那么至少有1个一等品的概率是________．
为了研究性别不同的高中学生是否爱好某项运动,运用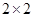
列联表进行独立性检验,经计算
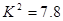,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别有关”.附:
 |
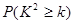0.050 |
0.010 |
0.001 |
 |
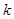3.841 |
6.635 |
10.828 |
姚明比赛时罚球命中率为90%，则他在3次罚球中罚失1次的概率是 ．
甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为a，再由乙猜甲刚才想的数字，把乙猜的数字记为b,且a,b 
{1，2，3，4},若|a
b| 
1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 （分式表示）
；
；
粤公网安备 44130202000953号