已知一个射手每次击中目标的概率为p= ,他在4次射击中,命中两次的概率为________,刚好在第二、第三两次击中目标的概率为________.
,他在4次射击中,命中两次的概率为________,刚好在第二、第三两次击中目标的概率为________.
某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为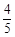 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为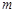 ,
,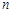 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记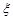 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为
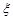 |
0 |
1 |
2 |
3 |
| P |
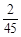 |
a |
d |
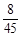 |
则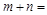 .
.
某厂生产的圆柱形零件的外径ε~N(4,0.25).质检人员从该厂生产的1000件零件中随机抽查一件,测得它的外径为5.7 cm.则该厂生产的这批零件是否合格________.
下面随机变量X的分布列不属于二项分布的是________.
①据中央电视台新闻联播报道,下周内在某网站下载一次数据,电脑被感染某种病毒的概率是0.65.设在这一周内,某电脑从该网站下载数据n次中被感染这种病毒的次数为X;②某射手射击击中目标的概率为p,设每次射击是相互独立的,从开始射击到击中目标所需要的射击次数为X;③某射手射击击中目标的概率为p,设每次射击是相互独立的,射击n次命中目标的次数为X;④位于某汽车站附近有一个加油站,汽车每次出站后到这个加油站加油的概率为0.6,国庆节这一天有50辆汽车开出该站,假设一天里汽车去该加油站加油是相互独立的,去该加油站加油的汽车数为X.
设随机变量X的分布列为P(X=k)=pk(1-p)1-k(k=0.1,0<p<1),则E(X)=________.
已知某位射手每次击中目标的概率为0.8,每次射击的结果相互独立,那么他在6次射击中,最有可能击中目标的次数为_________次.
姚明比赛时罚球命中率为90%,则他在3次罚球中罚失1次的概率是 .
某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%;如果失败,一年后将丧失全部资金的50%.下表是过去200例类似项目开发的实施结果:
| 投资成功 |
投资失败 |
| 192例 |
8例 |
则该公司一年后估计可获收益的数学期望是________元.
甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为a,再由乙猜甲刚才想的数字,把乙猜的数字记为b,且a,b  {1,2,3,4},若|a
{1,2,3,4},若|a b|
b|  1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 (分式表示)
1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 (分式表示)