高中数学正交试验设计方法试题

下列说法：
① 设有一批产品,其次品率为0.05,则从中任取200件,必有10件次品；
②抛100次硬币的试验,有51次出现正面.因此出现正面的概率是0.51；
③抛掷骰子100次,得点数是1的结果是18次,则出现1点的频率是；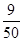
④抛掷两枚硬币，出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大
⑤有10个阄，其中一个代表奖品，10个人按顺序依次抓阄来决定奖品的归属，则摸奖的顺序对中奖率没有影响。
其中正确的有_____________。

已知椭圆的焦点为，在长轴上任取一点M，过M作垂直于的直线交椭圆于P，则使得的M点的概率为(  )

A．

B．

C．

D．

口袋内装有100个大小相同的红球、白球和黑球，其中有45个红球；从中摸出1个球，若摸出白球的概率为0.23，则摸出黑球的概率为____________．

若，则的值为（    ）

A．

B．

C．

D．

若X～B(n，p)，且E(X)＝6，V(X)＝3，则P(X＝1)的值为________．

某电视台有A、B两种智力闯关游戏，甲、乙、丙、丁四人参加，其中甲乙两人各自独立进行游戏A，丙丁两人各自独立进行游戏B.已知甲、乙两人各自闯关成功的概率均为，丙、丁两人各自闯关成功的概率均为.
(I )求游戏A被闯关成功的人数多于游戏B被闯关成功的人数的概率；
(II) 记游戏A、B被闯关成功的总人数为，求的分布列和期望.

甲、乙、丙三人在同一办公室工作，办公室只有一部电话机，给该机打进的电话是打给甲、乙、丙的概率分别是，在一段时间内该电话机共打进三个电话，且各个电话之间相互独立，则这三个电话中恰有两个是打给乙的概率是                (用分数作答)

在三次独立重复试验中，事件A在每次试验中发生的概率相同，若事件A至少发生一次的概率为，则事件A恰好发生一次的概率为（   ）

A．

B．

C．

D．

在15个村庄中,有7个村庄交通不太方便,现从中任意选10个村庄,用X表示10个村庄中交通不太方便的村庄数,下列概率中等于的是(    )

A．

B．

C．

D．

小王通过英语听力测试的概率是，他连续测试3次，那么其中恰有1次获得通过的概率是（  ）

A．

B．

C．

D．

某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下．记成绩不低于90分者为“成绩优秀”．

甲		乙
6	9	3 6 7 9 9
9 5 1 0	8	0 1 5 6
9 9 4 4 2	7	3 4 5 8 8 8
8 8 5 1 1 0	6	0 7 7
4 3 3 2	5	2 5

 
(1)在乙班样本中的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
(2)由以上统计数据填写下面列联表，并判断是否有90%的把握认为：“成绩优秀”与教学方式有关.

	甲班(A方式)	乙班(B方式)	总计
成绩优秀
成绩不优秀
总计

 
附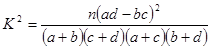：,其中n＝a＋b＋c＋d.)

P(K^2≥k)	0.25	0.15	0.10	0.05	0.025	0.01	0.005	0.001
k	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

 

在等差数列{a_n}中，a₄＝2，a₇＝－4.现从{a_n}的前10项中随机取数，每次取出一个数，取后放回，连续抽取3次，假定每次取数互不影响，那么在这三次取数中，取出的数恰好为两个正数和一个负数的概率为________(用数字作答)．

甲、乙两人各射击1次，击中目标的概率分别是和，假设两人射击目标是否击中相互之间没有影响，每人各次射击是否击中目标也没有影响．则两人各射击4次，甲恰好有2次击中目标且乙恰好有3次击中目标的概率为________．

两人射击命中目标的概率分别为现两人同时射击目标，则目标能被命中的概率为。（用数字作答）

有一批种子，每一粒发芽的概率为，播下粒种子，恰有粒发芽的概率为 (     )

A．	B．
C．	D．