高中数学平行线法选择题

设m，n是两条不同的直线，α，β是两个不同的平面，下列命题正确的是  （   ）

A．则

B．且，则

C．，则

D．，则

设m，n是两条不同的直线，、、是三个不同的平面，给出下列命题，正确的是（  ）.

A．若，，则

B．若，，则

C．若，，则

D．若，，，则

如图，AB为圆O的直径，点C在圆周上（异于点A，B），直线PA垂直于圆O所在的平面，点M为线段PB的中点．有以下四个命题：
①PA∥平面MOB；      ②OC⊥平面PAC；
③MO∥平面PAC；      ④平面PAC⊥平面PBC．
其中正确的命题是（ ）．

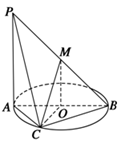
A．①②       B．①③       C．③④        D．②④

用a，b，c表示三条不同的直线，表示平面，给出下列命题：
①若
②若；
③若；
④若
其中真命题的序号是（     ）

A．①③

B．①④

C．②③

D．②④

如图四棱柱中，面，四边形为梯形，，且
过三点的平面记为，与的交点为，则以下四个结论：
①②③直线与直线相交；④四棱柱被平面分成的上下两部分的体积相
等，其中正确的个数为（  ）

A．1个

B．2个

C．3个

D．4个

以下说法中，正确的个数是（ ）
①平面内有一条直线和平面平行，那么这两个平面平行
②平面内有两条直线和平面平行，那么这两个平面平行
③平面内有无数条直线和平面平行，那么这两个平面平行
④平面内任意一条直线和平面都无公共点，那么这两个平面平行

A．0个

B．1个

C．2个

D．3个

下列各个图形中，异面直线的画法不妥的是（ ）

A．

B．

C．

D．

若空间中四条直线两两不同的直线，满足，则下列结论一定正确的是（   ）

A．		B．
C．	既不平行也不垂直	D．	的位置关系不确定

如图，在正四棱锥中，，，分别是，，的中点，动点在线段上运动时，下列四个结论：①；②；③；④．中恒成立的为（    ）

A．①③

B．③④

C．①②

D．②③④

已知命题p：m，n为直线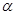，为平面，若m∥n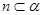，，则m∥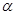；命题q：若a>b，则ac>bc，则下列命题为真命题的是（  ）

A．p或q

B．p且q

C．p或q

D．p且q

如图所示，在正方体中，点是棱上的一个动点，平面交棱于点．则下列命题中真命题的个数是（  ）
 
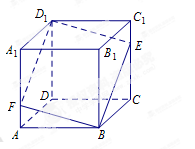
①存在点，使得//平面         
②存在点，使得平面
③对于任意的点，平面平面 
④对于任意的点，四棱锥的体积均不变

A．0个

B．1个

C．2个

D．3个

如图所示，正方体中，M、N、E、F分别是棱，，，的中点，用空间向量方法证明：平面AMN∥平面EFDB．

设是两条不同的直线，是三个不同的平面，有以下四个命题：
①  ②   ③   ④
其中正确的命题是（ ）

A．①④

B．②③

C．①③

D．②④

已知棱长为2的正方体，是过顶点圆上的一点，为中点，则与面所成角余弦值的取值范围是（   ）

A．

B．

C．

D．

已知是两条不同的直线，是三个不同的平面，则下列命题中正确的是

A．若	B．若
C．若	D．若