某同学使用计算器求
个数据的平均数时，错将其中一个数据
输入为
，那么由此求出的平均数减去实际平均数的值是 （ ）
A． |
B． |
C． |
D． |
为了研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：kPa）的分组区间为：[12，13），[13，14），[14，15），[15，16），[16，17]，将其按从左到右的顺序分别编号为第一组，第二组，
，第五组，右图是根据试验数据制成的频率分布直方图，已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为（ ）
| A．6 | B．8 | C．12 | D．18 |
（本小题满分14分）下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩（单位:分）．已知甲代表队数据的中位数为76，乙代表队数据的平均数是75．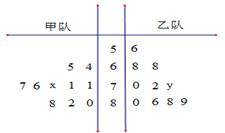
（1）求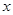
，
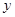的值；
（2）若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生，求抽到的学生中，甲队学生成绩不低于乙队学生成绩的概率；
（3）判断甲、乙两队谁的成绩更稳定，并说明理由（方差较小者稳定）．
某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们每场比赛得分的情况用如图所示的茎叶图表示，则甲、乙两名运动员的中位数分别是 （ ）
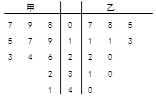
A． 、 |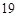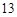
B．、 |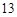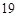
C． 、 |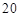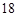
D．、 |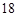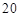
数据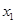
，
，
，
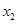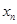的平均数为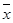
，方差为
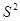，则数据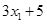
，
，，
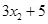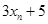的方差是（）
| A． |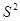
B． |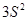
C． |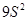
D． |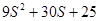
在2011年孝感高中“校园十佳歌手”大赛中，七位评委为一选手打出的分数如下：
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后，所剩数据的平均值和方差分别为（ ）
| A．92，2 | B．92，2．8 | C．93，2 | D．93，2．8 |
（本小题满分12分）某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，200），[220．240），[240，260），[260，280），[280，300）分组的频率分布直方图如图．
（1）求月平均用电量的众数和中位数；
（2）在月平均用电量为[220．240），[240，260），[260，280），[280，300）的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[240．260）的用户中应抽取多少户？
某工厂的10名工人生产同一零件，生产的件数分别为15,17,14,10,15,17,17,16,14,12，设其平均数为
，中位数为
，众数为
，则有（ ）
A． |
B． |
C． |
D． |
交通管理部门为了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为
，其中甲社区有驾驶员
人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为
，
，
，
，则这四个社区驾驶员的总人数为 ．
学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n且支出在[20,60）元的样本，其频率分布直方图如图所示，其中支出在[50,60）元的学生有30人，则n的值为（ ）
| A．1000 | B．900 | C．100 | D．90 |
下列说法中，正确的是（ ）
| A．数据5,4,4,3,5,2的众数是4 |
| B．一组数据的标准差是这组数据的方差的平方 |
| C．数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 |
| D．频率分布直方图中各小长方形的面积等于相应各组的频数 |
（本小题12分）根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2．5的年平均浓度不得超过35微克/立方米，PM2．5的24小时平均浓度不得超过75微克/立方米．某城市环保部门随机抽取了一居民区去年20天PM2．5的24小时平均浓度的监测数据，数据统计如下：
]
| 组别 |
PM2.5浓度（微克/立方米） |
频数（天） |
频率 |
| 第一组 |
 |
3 |
0.15 |
| 第二组 |
 |
12 |
0.6 |
| 第三组 |
 |
3 |
0.15 |
| 第四组 |
 |
2 |
0.1 |
（Ⅰ）从样本中PM2．5的24小时平均浓度超过50微克/立方米的5天中，随机抽取2天，求恰好有一天PM2．5的24小时平均浓度超过75微克/立方米的概率；
（Ⅱ）求样本平均数，并根据样本估计总体的思想，从PM2．5的年平均浓度考虑，判断该居民区的环境是否需要改进？说明理由．
学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n的样本，其频率分布直方图如图所示，其中支出在
元的同学有39人，则n的值为（ ）
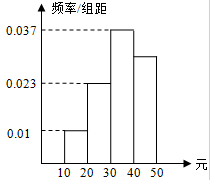
| A．100 | B．120 | C．130 | D．390 |
一组数据的平均数是2，方差是4，若将这组每个数据都加上10构成一组新数据，则这组新数据的平均数和标准差分别是（ ）
| A．12，2 | B．12，12 | C．8，2 | D．8，12 |
粤公网安备 44130202000953号
年元旦晚会举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的众数和中位数分别为（ ）