在正四面体P—ABC中,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )
| A.BC//平面PDF | B.DF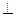 平面PAE 平面PAE |
C.平面PDF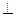 平面ABC 平面ABC |
D.平面PAE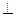 平面ABC 平面ABC |
已知两个平面垂直,下列命题 一个平面内已知直线必垂直于另一个平面内的任意一条直线.
一个平面内已知直线必垂直于另一个平面内的任意一条直线. 一个平面内的已知直线必垂直于另一个平面的无数条直线.
一个平面内的已知直线必垂直于另一个平面的无数条直线. 一个平面内的任一条直线必垂直于另一个平面.
一个平面内的任一条直线必垂直于另一个平面. 过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
其中正确的个数是( )
| A.3 | B.2 | C.1 | D.0 |
(本小题满分16分)如图,正四棱锥P-ABCD中,O是底面正方形的中心,E是PC的中点,求证
(1)PA∥平面BDE
(2)平面PAC  平面BDE
平面BDE
(设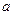 、
、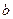 是两条不同的直线,α、β是两个不同的平面,则下列四个命题
是两条不同的直线,α、β是两个不同的平面,则下列四个命题
①若 ②若
②若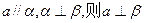
③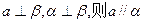 ④
④
其中正确的命题的个数是()
| A.0个 | B.1个 | C.2个 | D.3个 |
下面四个命题:
①“直线a∥直线b”的充要条件是“a平行于b所在的平面”;
②“直线 ⊥平面
⊥平面 内所有直线”的充要条件是“
内所有直线”的充要条件是“ ⊥平面
⊥平面 ”;
”;
③“直线a、b为异面直线”的充分不必要条件是“直线a、b不相交”;
④“平面 ∥平面
∥平面 ”的必要不充分条件是“
”的必要不充分条件是“ 内存在不共线三点到
内存在不共线三点到 的距离相等”;
的距离相等”;
其中正确命题的序号是
| A.①② | B.②③ | C.③④ | D.②④ |
a、b是两条异面直线,则“a⊥b”是“存在经过a且与b垂直的平面”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件  既不充分也不必要条件
既不充分也不必要条件
如图甲,在△ABC中,AB⊥AC,AD⊥BC,
D是垂足,则AB2=BD·BC,该结论称为射
影定理。如图乙,在三棱锥A—BCD中,
AD⊥平面ABC,AO⊥平面BCD,O为垂
足,且O在△BCD内,类比射影定理,探
究S△BCO、S△BCD、S△ABC这三者之间满足的
关系式是 。
如图,在正方体ABCD—A1B1C1D1中,若E是AD的中点,则直线A1B与直线C1E的位置关系是( )w.
| A.平行 | B.相交 |
| C.共面 | D.垂直 |