设 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给定下列四个命题:
是两个不重合的平面,给定下列四个命题:
①若 ,
, ,则
,则 ;
;
②若 ,
, ,则
,则 ;
;
③若 ,
, ,则
,则 ;
;
④若 ,
, ,
, ,则
,则 .
.
其中真命题的序号为 .
如图是棱长为 的正方体的平面展开图,则在原正方体中,
的正方体的平面展开图,则在原正方体中,
① 平面
平面 ;
;
② 平面
平面 ;
;
③CN与BM成 角;
角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是____ ____。 (写出所有正确命题的序号)
在 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为________________.
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点
上有两个动点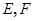 ,且
,且 ,则下列结论中正确的有 .(填写你认为正确的序号)
,则下列结论中正确的有 .(填写你认为正确的序号)

① ;
;
② ;
;
③若 为
为 上的一动点,则三棱锥
上的一动点,则三棱锥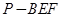 的体积为定值;
的体积为定值;
④在空间与直线 都相交的直线只有1条。
都相交的直线只有1条。
[2012·辽宁高考]已知正三棱锥P-ABC,点P,A,B,C都在半径为 的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
三棱锥 中,
中, 若
若 ,
, 是该三棱锥外部(不含表面)的一点,给出下列四个命题,
是该三棱锥外部(不含表面)的一点,给出下列四个命题,
① 存在无数个点 ,使
,使 ;
;
② 存在唯一点 ,使四面体
,使四面体 为正三棱锥;
为正三棱锥;
③ 存在无数个点 ,使
,使 ;
;
④ 存在唯一点 ,使四面体
,使四面体 有三个面为直角三角形.
有三个面为直角三角形.
其中正确命题的序号是 .
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:
①直线BE与直线CF异面;
②直线BE与直线AF异面;
③直线EF∥平面PBC;
④平面BCE⊥平面PAD.
其中正确的有__________.
如图,在三棱锥 中,
中, ,
, ,平面
,平面 平面
平面 ,
, 为
为 中点,点
中点,点 分别为线段
分别为线段 上的动点(不含端点),且
上的动点(不含端点),且 ,则三棱锥
,则三棱锥 体积的最大值为________.
体积的最大值为________.
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中正确的是 .
①BM|是定值
②点M在某个球面上运动
③存在某个位置,使DE⊥A1 C
④存在某个位置,使MB//平面A1DE
已知空间直角坐标系o﹣xyz中的点A的坐标为(1,1,1),平面α过点A且与直线OA垂直,动点P(x,y,z)是平面α内的任一点,则点P的坐标满足的条件是 .
设l,m是不同的直线,α,β,γ是不同的平面,则下列命题正确的是______________.
①若l⊥m,m⊥α,则l⊥α或 l∥α
②若l⊥γ,α⊥γ,则l∥α或 l α
α
③若l∥α,m∥α,则l∥m或 l与m相交
④若l∥α,α⊥β,则l⊥β或l β
β
如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点,设异面直线EM与AF所成的角为 ,则
,则 的最大值为 .
的最大值为 .

 是异面直线,下面四个命题:
是异面直线,下面四个命题:
①过 至少有一个平面平行于
至少有一个平面平行于 ;
;
②过 至少有一个平面垂直于
至少有一个平面垂直于 ;
;
③至多有一条直线与 都垂直;
都垂直;
④至少有一个平面与 都平行.
都平行.
其中正确命题的个数是