已知 是直线,
是直线,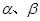 是平面,下列命题中:
是平面,下列命题中:
①若 垂直于
垂直于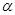 内两条直线,则
内两条直线,则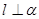 ;
;
②若 平行于
平行于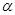 ,则
,则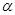 内可有无数条直线与
内可有无数条直线与 平行;
平行;
③若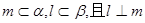 ,则
,则 ;
;
④若m⊥n,n⊥l则m∥l;
⑤若 ,则
,则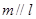 ;
;
正确的命题序号为__________.
设 是空间的不同直线或不同平面,下列条件中能保证“若
是空间的不同直线或不同平面,下列条件中能保证“若 ,且
,且 ,则
,则 ”为真命题的是 . (填所正确条件的代号)
”为真命题的是 . (填所正确条件的代号)
① 为直线;
为直线;
② 为平面;
为平面;
③ 为直线,
为直线, 为平面;
为平面;
④ 为直线,
为直线, 为平面.
为平面.
下列命题中,真命题是 (将真命题前面的编号填写在横线上).
①已知平面 、
、 和直线
和直线 、
、 ,若
,若 ,
, 且
且 ,则
,则 .
.
②已知平面 、
、 和两异面直线
和两异面直线 、
、 ,若
,若 ,
, 且
且 ,
, ,则
,则 .
.
③已知平面 、
、 、
、 和直线
和直线 ,若
,若 ,
, 且
且 ,则
,则 .
.
④已知平面 、
、 和直线
和直线 ,若
,若 且
且 ,则
,则 或
或 .
.
在四棱锥P—ABCD中,侧面PAD、侧面PCD与底成ABCD都垂直,底面是边长为3的正方形,PD=4,则四棱锥P—ABCD的全面积为 .
如图,点P在正方体 的面对角线
的面对角线 上运动,则下列四个命题:①三棱锥
上运动,则下列四个命题:①三棱锥 的体积不变; ②
的体积不变; ② ∥面
∥面 ; ③
; ③ ; ④面
; ④面 面
面 。其中正确的命题的序号是_______________(写出所有你认为正确结论的序号)
。其中正确的命题的序号是_______________(写出所有你认为正确结论的序号)
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是 .(填写正确命题的序号)
①若m∥n,m⊥β,则 n⊥β;
②若m∥n,m∥β,则n∥β;
③若m∥α,m∥β,则α∥β;
④若n⊥α,n⊥β,则α⊥β.
设 为空间的两条直线,
为空间的两条直线, 为空间的两个平面,给出下列命题:
为空间的两个平面,给出下列命题:
①若

 ,
,

 , 则
, 则

 ;
;
②若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则

 ;
;
③若

 ,
,

 ,则
,则

 ;
;
④若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则

 ;
;
上述命题中,其中假命题的序号是 .
已知正三棱锥P-ABC,点P,A,B,C都在半径为 的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为__________.
的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为__________.
设 为两个不重合的平面,
为两个不重合的平面, 为两条不重合的直线,给出下列四个命题:
为两条不重合的直线,给出下列四个命题:
①若 ,则
,则 ;[
;[
②若 ,则
,则 ;
;
③若 则
则 ;
;
④若 与
与 相交且不垂直,则
相交且不垂直,则 与
与 一定不垂直.
一定不垂直.
其中,所有真命题的序号是 .
a,b,c表示直线,M表示平面,给出下列四个命题:
①若a∥M,b∥M,则a∥b;
②若b M,a∥b,则a∥M;
M,a∥b,则a∥M;
③若a⊥c,b⊥c,则a∥b;
④若a⊥M,b⊥M,则a∥b.
⑤a⊥M,b M,若b∥M,则b⊥a
M,若b∥M,则b⊥a
其中正确命题的序号是 .