已知直线: (
( 为给定的正常数,
为给定的正常数, 为参数,
为参数, )构成的集合为S,给出下列命题:
)构成的集合为S,给出下列命题:
①当 时,
时, 中直线的斜率为
中直线的斜率为 ;
;
② 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.
③当 时,存在某个定点,该定点到
时,存在某个定点,该定点到 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当 >
> 时,
时, 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为 ;
;
其中正确的是 (写出所有正确命题的编号).
若直线经过点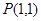 和点
和点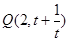 ,其中
,其中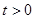 ,则该直线的倾斜角的取值范围是( ).
,则该直线的倾斜角的取值范围是( ).
A.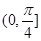 B
B 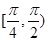 C.
C.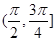 D.
D.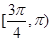
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y= x上时,求直线AB的方程.
x上时,求直线AB的方程.
已知线段PQ两端点的坐标分别为(-1,1)、(2,2),若直线l:x+my+m=0与线段PQ有交点,求m的取值范围.
已知直线PQ的斜率为- ,将直线绕点P顺时针旋转60°所得的直线的斜率是________.
,将直线绕点P顺时针旋转60°所得的直线的斜率是________.
直线xcosα+ y+2=0的倾斜角的取值范围是( )
y+2=0的倾斜角的取值范围是( )
A.[- , , ] ] |
B.[ , , ] ] |
C.[0, ]∪[ ]∪[ ,π) ,π) |
D.[0, ]∪[ ]∪[ ,π] ,π] |
已知射线l1:y=4x(x≥0)和点P(6,4),试在l1上求一点Q使得PQ所在直线l和l1以及直线y=0在第一象限围成的面积达到最小值,并写出此时直线l的方程.
[2014·湖南郴州]若直线m被两平行线l1:x-y+1=0与l2:x-y+3=0所截得的线段的长为2 ,则m的倾斜角可以是
,则m的倾斜角可以是
①15°;②30°;③45°;④60°;⑤75°.
其中正确答案的序号是________.(写出所有正确答案的序号)
[2014·汕头质检]若三点A(2,3),B(3,2),C( ,m)共线,则实数m=________.
,m)共线,则实数m=________.
已知椭圆 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率 , 直线
, 直线 交椭圆于M,N两点.
交椭圆于M,N两点.
(1)若直线 的方程为y=x-4,求弦MN的长:
的方程为y=x-4,求弦MN的长:
(2)如果 BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线 的方程.
的方程.
已知椭圆 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率 , 直线
, 直线 交椭圆于M,N两点.
交椭圆于M,N两点.
(1)若直线 的方程为y=x-4,求弦MN的长:
的方程为y=x-4,求弦MN的长:
(2)如果 BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线 的方程.
的方程.
设 是椭圆
是椭圆 上不关于坐标轴对称的两个点,直线
上不关于坐标轴对称的两个点,直线 交
交 轴于点
轴于点 (与点
(与点 不重合),O为坐标原点.
不重合),O为坐标原点.
(1)如果点 是椭圆
是椭圆 的右焦点,线段
的右焦点,线段 的中点在y轴上,求直线AB的方程;
的中点在y轴上,求直线AB的方程;
(2)设 为
为 轴上一点,且
轴上一点,且 ,直线
,直线 与椭圆
与椭圆 的另外一个交点为C,证明:点
的另外一个交点为C,证明:点 与点
与点 关于
关于 轴对称.
轴对称.