已知直线：
（
为给定的正常数，
为参数，
）构成的集合为S,给出下列命题：
①当
时，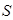
中直线的斜率为
；
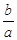②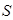中的所有直线可覆盖整个坐标平面．
③当
时，存在某个定点，该定点到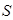中的所有直线的距离均相等；
④当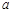
＞
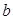时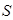，中的两条平行直线间的距离的最小值为
；
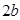其中正确的是 （写出所有正确命题的编号）．
与
平行；
与
是异面直线；
角；
与
是异面直线；
是定义在
上的偶函数，且当
时，
，则当
时，
．
，（
是
上的减函数，则
的取值范围是 ．
，则
．相关知识点
推荐套卷
已知直线：（为给定的正常数，为参数，）构成的集合为S,给出下列命题：
①当时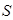，中直线的斜率为；
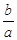②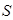中的所有直线可覆盖整个坐标平面．
③当时，存在某个定点，该定点到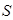中的所有直线的距离均相等；
④当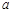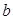＞时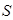，中的两条平行直线间的距离的最小值为；
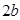其中正确的是 （写出所有正确命题的编号）．
粤公网安备 44130202000953号