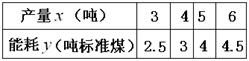
小明同学根据右表记录的产量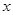 (吨)与能耗
(吨)与能耗 (吨标准煤)对应的四组数据,用最小二乘法求出了
(吨标准煤)对应的四组数据,用最小二乘法求出了 关于
关于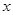 的线性回归方程
的线性回归方程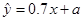 ,据此模型预报产量为7万吨时能耗为( )
,据此模型预报产量为7万吨时能耗为( )
A. |
B.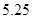 |
C. |
D.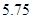 |
已知边长为3的正方形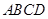 与正方形
与正方形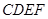 所在的平面互相垂直,
所在的平面互相垂直,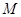 为线段
为线段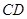 上的动点(不含端点),过
上的动点(不含端点),过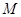 作
作 交
交 于
于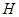 ,作
,作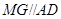 交
交 于
于 ,连结
,连结 .设
.设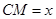
 ,则下面四个图象中大致描绘了三棱锥
,则下面四个图象中大致描绘了三棱锥 的体积
的体积 与变量
与变量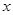 变化关系的是
变化关系的是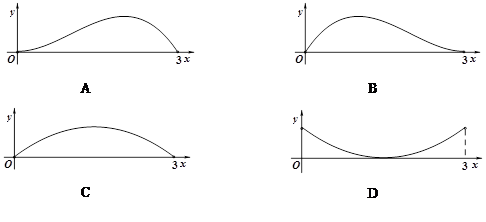
废品率 和每吨生铁成本
和每吨生铁成本 (元)之间的回归直线方程为
(元)之间的回归直线方程为 ,这表明 ( )
,这表明 ( )
A. 与 与 的相关系数为2 的相关系数为2 |
B. 与 与 的关系是函数关系的充要条件是相关系数为1 的关系是函数关系的充要条件是相关系数为1 |
| C.废品率每增加1%,生铁成本增加258元 |
| D.废品率每增加1%,生铁成本平均每吨增加2元 |
已知x,y取值如下表:
| x |
0 |
1 |
4 |
5 |
6 |
8 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.3 |
从所得的散点图分析可知:y与x线性相关,且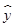 =0.95x+a,则a=( ).
=0.95x+a,则a=( ).
A.1.30 B.1.45 C.1.65 D.1.80
若回归直线方程的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( ).
A.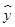 =1.23x+4 =1.23x+4 |
B.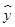 =1.23x+5 =1.23x+5 |
C.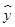 =1.23x+0.08 =1.23x+0.08 |
D.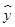 =0.08x+1.23 =0.08x+1.23 |
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A.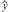 =-10x+200 =-10x+200 |
B.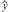 =10x+200 =10x+200 |
C.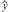 =-10x-200 =-10x-200 |
D. =10x-200 =10x-200 |
废品率 和每吨生铁成本
和每吨生铁成本 (元)之间的回归直线方程为
(元)之间的回归直线方程为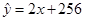 ,这表明 ( )
,这表明 ( )
A. 与 与 的相关系数为2 的相关系数为2 |
B. 与 与 的关系是函数关系的充要条件是相关系数为1 的关系是函数关系的充要条件是相关系数为1 |
| C.废品率每增加1%,生铁成本增加258元 |
| D.废品率每增加1%, 生铁成本平均每吨增加2元 |
观察下面频率等高条形图,其中两个分类变量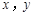 之间关系最强的是( )
之间关系最强的是( )
A. B. C. D.
设有一个直线回归方程为 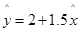 ,则变量x 增加一个单位时( )
,则变量x 增加一个单位时( )
| A.y 平均增加 1.5 个单位 | B.y 平均增加 2 个单位 |
| C.y 平均减少 1.5 个单位 | D.y 平均减少 2 个单位 |
由一组数据(x1,y1)、(x2、y2)、 、(xn,yn)得到的线性回归方程为y=a+bx,则下列说法正确的是( )
A.直线y=a+bx必过点( , , ) ) |
| B.直线y=a+bx至少经过点(x1,y1)、(x2,y2)、 、(xn,yn)中的一点 |
| C.直线y=a+bx是由(x1,y1)、(x2、y2)、 、(xn,yn)中的两点确定的 |
| D.(x1,y1)、(x2,y2)、 、(xn、yn)这n个点到直线y=a+bx的距离之和最小 |
某公司2005~2010年的年利润x(单位:百万元)与年广告支出y(单位:百万元)的统计资料如表所示:
| 年份 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
| 利润x |
12.2 |
14.6 |
16 |
18 |
20.4 |
22.3 |
| 支出y |
0.62 |
0.74 |
0.81 |
0.89 |
1 |
1.11 |
根据统计资料,则( )
A.利润中位数是16,x与y有正线性相关关系
B.利润中位数是18,x与y有负线性相关关系
C.利润中位数是17,x与y有正线性相关关系
D.利润中位数是17,x与y有负线性相关关系
某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
| 气温x(℃) |
18 |
13 |
10 |
-1 |
| 用电量y(度) |
24 |
34 |
38 |
64 |
由表中数据得线性回归方程 =
=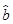 x+
x+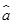 中
中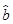 ≈-2,预测当气温为-4℃时,用电量的度数约为( )
≈-2,预测当气温为-4℃时,用电量的度数约为( )
A.58 B.66 C.68 D.70
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为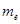 ,众数为
,众数为 ,平均值为
,平均值为 ,则( )
,则( )
A. 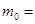  |
B. 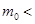  |
C. 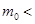  |
D.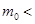   |
某科研所共有职工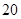 人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
A.年龄数据的中位数是 ,众数是 ,众数是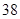 |
| B.年龄数据的中位数和众数一定相等 |
C.年龄数据的平均数 |
| D.年龄数据的平均数一定大于中位数 |