废品率x%和每吨生铁成本y(元)之间的回归直线方程为y=256+3x,表明( )
| A.废品率每增加1%,生铁成本增加259元. | B.废品率每增加1%,生铁成本增加3元. |
| C.废品率每增加1%,生铁成本每吨增加3元. | D.废品率不变,生铁成本为256元. |
为了评价某个电视栏目的改革效果,在改革前后分别从某居民点抽取了1000位居民进行调查,经过计算得K2 4.358,根据这一数据分析,下列说法正确的是( )
4.358,根据这一数据分析,下列说法正确的是( )
| A.有95%的人认为该栏日优秀 |
| B.有95%的人认为该栏目是否优秀与改革有关系 |
| C.有95%的把握认为电视栏目是否优秀与改革有关系 |
| D.没有理由认为电视栏目是否优秀与改革有关系 |
对两个变量 和
和 进行回归分析,得到一组样本数据:
进行回归分析,得到一组样本数据: ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
A.由样本数据得到的回归方程 必过样本中心 必过样本中心 |
| B.残差平方和越小的模型,拟合的效果越好 |
C.用相关指数 来刻画回归效果, 来刻画回归效果, 越小,说明模型的似合效果越好 越小,说明模型的似合效果越好 |
D.若变量y和x之间的相关系数为 ,则变量y和x之间具有线性相关关系 ,则变量y和x之间具有线性相关关系 |
对变量x, y 有观测数据(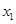 ,
,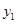 )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 |
| B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 |
| D.变量x 与y 负相关,u 与v 负相关 |
一名小学生的年龄和身高(单位:cm)的数据如下:
| 年龄X |
6 |
7 |
8 |
9 |
| 身高Y |
118 |
126 |
136 |
144 |
由散点图可知,身高y与年龄x之间的线性回归直线方程为 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A. 154 B. 153 C. 152 D. 151
两个变量x,y与其线性相关系数r有下列说法
(1)若r>0,则x增大时,y也相应增大;
(2)若r<0,则x增大时,y也相应增大;
(3)若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上,其中正确的有 ( )
| A.①② | B.②③ | C.①③ | D.①②③ |
为了解儿子身高与其父亲身高的关系,随机抽取5对父子身高数据如下
| 父亲身高x(cm) |
174 |
176 |
176 |
176 |
178 |
| 儿子身高y(cm) |
175 |
175 |
176 |
177 |
177 |
则y对x的线性回归方程为 ( )
A. B.
B.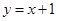 C.
C. D.
D.
下面是2×2 列联表
| x y |
y 1 |
y 2 |
合计 |
| x1 |
a |
21 |
73 |
| x2 |
2 |
25 |
27 |
| 合计 |
b |
46 |
100 |
则表中 a 、b 处的值分别为( )
A.94 、96 B.52 、50 C.52 、54 D.54 、52
观察下面频率等高条形图,其中两个分类变量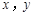 之间关系最强的是( )
之间关系最强的是( )
A. B. C. D.
某市对上下班交通情况作抽样调查,作出上下班时间各抽取 的12辆机动车行驶时速(单位:km/h)的茎叶图如图.则上、下班行驶时速的中位数分别为()
| A.28与28.5 | B.29与28.5 | C.28与27.5 | D.29与27.5 |
某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )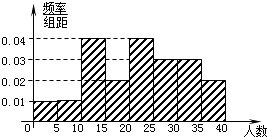

对具有线性相关关系的变量x,y有一组观测数据(xi,yi)( i=1,2,…,8),其回归直线方程是 =
=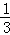 x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
A.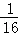 |
B.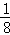 |
C.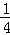 |
D. |