对变量x, y 有观测数据(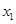 ,
,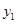 )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 |
| B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 |
| D.变量x 与y 负相关,u 与v 负相关 |
一名小学生的年龄和身高(单位:cm)的数据如下:
| 年龄X |
6 |
7 |
8 |
9 |
| 身高Y |
118 |
126 |
136 |
144 |
由散点图可知,身高y与年龄x之间的线性回归直线方程为 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A. 154 B. 153 C. 152 D. 151
某车间加工零件的数量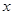 与加工时间
与加工时间 的统计数据如下表:
的统计数据如下表:
零件数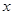 (个) (个) |
10 |
20 |
30 |
加工时间 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程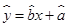 中的
中的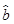 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
如图,有  组
组 数据,去掉 组(即填A,B,C,D,E中的某一个)
数据,去掉 组(即填A,B,C,D,E中的某一个)
后,剩下的四组数据的线性相关系数最大。( )
A. |
B. |
C. |
D. |
某车间加工零件的数量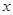 与加工时间
与加工时间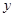 的统计数据如下表:
的统计数据如下表:
现已求得上表数据的回归方程 中的
中的 的值为0.9,则据此回归模型可以预测,加工90个零件所需要的加工时间约为( )
的值为0.9,则据此回归模型可以预测,加工90个零件所需要的加工时间约为( )
| A.93分钟 | B.94分钟 | C.95分钟 | D.96分钟 |
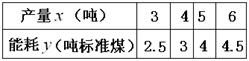
小明同学根据右表记录的产量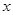 (吨)与能耗
(吨)与能耗 (吨标准煤)对应的四组数据,用最小二乘法求出了
(吨标准煤)对应的四组数据,用最小二乘法求出了 关于
关于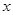 的线性回归方程
的线性回归方程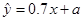 ,据此模型预报产量为7万吨时能耗为( )
,据此模型预报产量为7万吨时能耗为( )
A. |
B.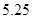 |
C. |
D.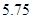 |
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1的 为0.975 为0.975 |
B.模型2的 为0.79 为0.79 |
C.模型3的 为0.55 为0.55 |
D.模型4的 为0.25 为0.25 |
对变量 有观测数据(
有观测数据( ,
, )(
)( ),得散点图1;对变量
),得散点图1;对变量 有观测数据(
有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
| A.变量x 与y 正相关,u 与v 正相关 | B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 | D.变量x 与y 负相关,u 与v 负相关 |
已知x,y取值如下表:
| x |
0 |
1 |
4 |
5 |
6 |
8 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.3 |
从所得的散点图分析可知:y与x线性相关,且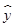 =0.95x+a,则a=( ).
=0.95x+a,则a=( ).
A.1.30 B.1.45 C.1.65 D.1.80
设某大学的女生体重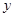 (单位:
(单位: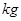 )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据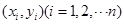 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为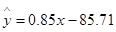 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.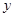 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心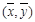 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
已知变量x与y正相关,且由观测数据算得样本平均数线性回归方程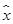 =3,
=3, =3.5,则由该观测数据算得的线性回归方程可能是( )
=3.5,则由该观测数据算得的线性回归方程可能是( )
A. =-2x+9.5 =-2x+9.5 |
B. =2x-2.4 =2x-2.4 |
C. =0.4x+2.3 =0.4x+2.3 |
D. =-0.3x+4.4 =-0.3x+4.4 |
具有线性相关关系的变量x,y ,满足一组数据如右表所示.若 与
与 的回归直线方程为
的回归直线方程为 ,则m的值是( )
,则m的值是( )
 |
0 |
1 |
2 |
3 |
 |
-1 |
1 |
m |
8 |
A. 4 B. C. 5 D. 6
C. 5 D. 6