某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误的一个是( )
| A.甲的极差是29 | B.乙罚球比甲更稳定 |
| C.甲罚球的命中率比乙高 | D.甲的中位数是24 |
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每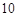 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②若两个变量的线性相关性越强,则相关系数的绝对值越接近于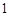 ;
;
③在某项测量中,测量结果 服从正态分布
服从正态分布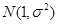
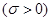 ,若
,若 位于区域
位于区域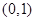 内的概率为
内的概率为 ,则
,则 位于区域
位于区域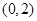 内的概率为
内的概率为 ;
;
④对分类变量 与
与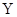 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“ 与
与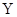 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )
| A.①④ | B.②④ | C.①③ | D.②③ |
已知 的取值如下表:
的取值如下表:
根据上表提供的数据,求出y对x的线性回归方程为 ,则表中的数据a的值为( )
,则表中的数据a的值为( )
| A.4.6 | B.4.8 | C.5.45 | D.5.55 |
某工厂为了对新研发的一种产品进行合理定价,交该产品按事先拟定的价格进行试销,得到如下数据:
单价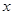 (元) (元) |
4 |
5 |
6 |
7 |
8 |
9 |
销量 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
由表中数据,求得线性回归方程为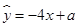 ,若在这些样本点中任取一点,则它在回归直线左下方的概率为
,若在这些样本点中任取一点,则它在回归直线左下方的概率为
A.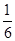 B.
B.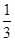 C.
C. D.
D.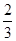
设有一个直线回归方程为 ,则变量
,则变量 增加一个单位时 ( )
增加一个单位时 ( )
A. 平均增加1.5个单位 平均增加1.5个单位 |
B. 平均增加2个单位 平均增加2个单位 |
C. 平均减少1.5个单位 平均减少1.5个单位 |
D. 平均减少2个单位 平均减少2个单位 |
已知关于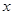 与
与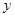 之间的一组数据:
之间的一组数据:
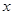 |
2 |
3 |
3 |
6 |
6 |
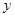 |
2 |
6 |
6 |
10 |
11 |
则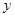 与
与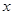 的线性回归方程
的线性回归方程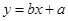 必过点( )
必过点( )
A.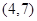 B.
B.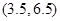 C.
C.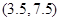 D.
D.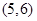
以下命题中:①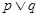 为假命题,则
为假命题,则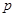 与
与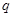 均为假命题
均为假命题
②对具有线性相关的变量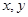 有一组观测数据
有一组观测数据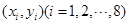 ,其回归直线方程是
,其回归直线方程是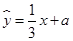 ,且
,且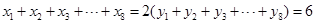 ,则实数
,则实数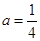
③对于分类变量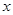 与
与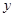 它们的随机变量
它们的随机变量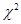 的观测值
的观测值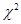 来说
来说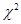 越小.“
越小.“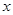 与
与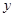 有关联”的把握程度越大
有关联”的把握程度越大
④已知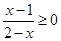 ,则函数
,则函数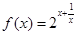 的最小值为16. 其中真命题的个数为 ( )
的最小值为16. 其中真命题的个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) |
3.0 |
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
| 销量y(瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知的关系符合线性回归方程 ,其中
,其中 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
某学生四次模拟考试时,其英语作文的减分情况如下表:
| 考试次数x |
1 |
2 |
3 |
4 |
| 所减分数y |
4.5 |
4 |
3 |
2.5 |
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为
A.
B.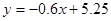
C.
D.
下列说法中正确的是( )
A.若分类变量 和 和 的随机变量 的随机变量 的观测值 的观测值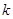 越大,则“ 越大,则“ 与 与 相关”的可信程度越小 相关”的可信程度越小 |
B.对于自变量 和因变量 和因变量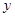 ,当 ,当 取值一定时, 取值一定时,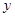 的取值具有一定的随机性, 的取值具有一定的随机性, , ,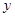 间的这种非确定关系叫做函数关系 间的这种非确定关系叫做函数关系 |
C.相关系数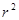 越接近1,表明两个随机变量线性相关性越弱 越接近1,表明两个随机变量线性相关性越弱 |
D.若分类变量 与 与 的随机变量 的随机变量 的观测值 的观测值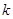 越小,则两个分类变量有关系的把握性越小 越小,则两个分类变量有关系的把握性越小 |
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是=-0.7x+a,则a等于( )
| A.10.5 | B.5.15 | C.5.2 | D.5.25 |
容量为100的样本数据,按从小到大的顺序分为8组,如下表:
第三组的频数和频率分别是 ( )
A. 和0.14 和0.14 |
B.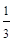 和 和 |
C.14和0.14 | D.0.14和14 |