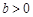已知变量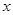 与
与 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
,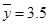 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.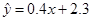 |
B.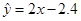 |
C.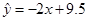 |
D.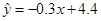 |
若样本 +2,
+2, +2, ,
+2, , +2的平均数为10,方差为3,则样本2
+2的平均数为10,方差为3,则样本2 +3,2
+3,2 +3,… ,2
+3,… ,2 +3,
+3,
的平均数、方差、标准差是( )
A.19,12, |
B.23,12, |
C.23,18, |
D.19,18, |
某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程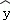 =
=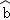 x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
58 |
A.112.1万元 B.113.1万元 C.111.9万元 D.113.9万元
根据如图样本数据得到的回归方程为 =bx+a,若样本点的中心为
=bx+a,若样本点的中心为 .则当x每增加1个单位时,y就( )
.则当x每增加1个单位时,y就( )

| A.增加1.4个单位 | B.减少1.4个单位 |
| C.增加7.9个单位 | D.减少7.9个单位 |
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程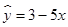 ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归直线方程 必过
必过 ;
;
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系;
其中错误的个数是( )
| A.0 | B.1 | C.2 | D.3 |
某产品在某零售摊位上的零售价x(元)与每天的销售量y(个)统计如下表:据上表可得回归直线方程 =b
=b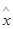 +a中的b=-4,据此模型预计零售价定为15元时,销售量为 ( )
+a中的b=-4,据此模型预计零售价定为15元时,销售量为 ( )
| A.48 | B.49 | C.50 | D.51 |
对具有线性相关关系的变量 ,
,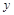 测得一组数据如下表:
测得一组数据如下表:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
20 |
40 |
60 |
80 |
100 |
根据上表,利用最小二乘法得到它们的回归直线方程为 .据此模型预测
.据此模型预测 时,
时,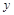 的估计值为( )
的估计值为( )
A. 320 B. 320.5 C. 322.5 D. 321.5
以下有关线性回归分析的说法不正确的是
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值 最小的a,b的值 |
| C.相关系数r越小,表明两个变量相关性越弱 |
D.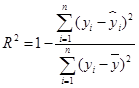 越接近1,表明回归的效果越好 越接近1,表明回归的效果越好 |
甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性做实验,并用回归分析方法分别求得相关系数r与残差平方和m如下表:
| |
甲 |
乙 |
丙 |
丁 |
| R |
0.82 |
0.78 |
0.69 |
0.85 |
| M |
106 |
115 |
124 |
103 |
则哪位同学的实验结果体现A、B两变量有更强的线性相关关系.
A.甲 B.乙 C.丙 D.丁
某产品的广告费用x与销售额y的统计数据如表:
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程 ,其中
,其中 =9.4,据此模型预报广告费用为6万元时,销售额为 ( ).
=9.4,据此模型预报广告费用为6万元时,销售额为 ( ).
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是 ( )
A.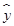 =-10x+200 =-10x+200 |
B.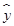 =10x+200 =10x+200 |
C.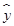 =-10x-200 =-10x-200 |
D.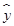 =10x-200 =10x-200 |
下表为某班5位同学身高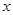 (单位:cm)与体重
(单位:cm)与体重 (单位kg)的数据,
(单位kg)的数据,
| 身高 |
170 |
171 |
166 |
178 |
160 |
| 体重 |
75 |
80 |
70 |
85 |
65 |
若两个量间的回归直线方程为 ,则
,则 的值为( )
的值为( )
A.-122.2 B.-121.04 C.-91 D.-92.3
变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4)(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2)(13,1),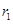 表示变量Y与X之间的线性相关系数,
表示变量Y与X之间的线性相关系数,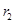 表示变量V与U之间的线性相关系数,则( )
表示变量V与U之间的线性相关系数,则( )
A.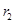 < <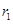 <0 <0 |
B.0<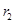 < <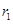 |
C.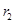 <0< <0<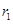 |
D.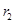 = =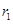 |
根据如下样本数据
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4.0 |
2.5 |
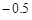 |
0.5 |
 |
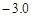 |
得到的回归方程为 ,则 ( )
,则 ( )
A.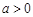 ,
, B.
B.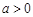 ,
,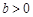
C.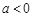 ,
, D.
D.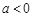 ,
,