一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归直线方程为 ,据此可以预测这个孩子10岁时的身高,则正确的叙述是
,据此可以预测这个孩子10岁时的身高,则正确的叙述是
| A.身高一定是145.83cm | B.身高超过146.00cm |
| C.身高低于145.00cm | D.身高在145.83cm左右 |
观察两个相关变量的如下数据:
 |
-1 |
-2 |
-3 |
-4 |
-5 |
5 |
4 |
3 |
2 |
1 |
 |
-0.9 |
-2 |
-3.1 |
-3.9 |
-5.1 |
5 |
4.1 |
2.9 |
2.1 |
0.9 |
则两个变量间的回归直线方程为 ( )
A. |
B. |
C. |
D.  |
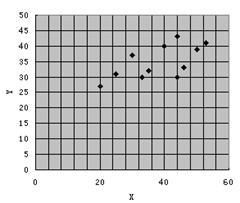
某次数学测试分为选择题与非选择题两部分,
右边的散点图中每个点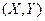 表示一位学生在
表示一位学生在
这两部分的得分,其中 表示该生选择题得
表示该生选择题得
分, 表示该生非选择题得分,设
表示该生非选择题得分,设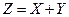 表
表
示该生的总分,现有11位学生的得分数据,根
据散点图,下列判断正确的是( )
A. 的方差< 的方差< 的方差 的方差 |
B. 的中位数> 的中位数> 的中位数 的中位数 |
C. 的众数< 的众数< 的众数 的众数 |
D. 的中位数= 的中位数= 的中位数+ 的中位数+ 的中位数 的中位数 |
体育课上,八年级一班两个组各10人参加立定跳远,要判断哪一组成绩比较整齐,通常需要知道这两个组立定跳远成绩的( )
| A.频率分布 | B.平均数 | C.方差 | D.众数 |
为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了50人,得到如下结果(单位:人)
| |
不患肺癌 |
患肺癌 |
合计 |
| 不吸烟 |
24 |
6 |
30 |
| 吸烟 |
6 |
14 |
20 |
| 合计 |
30 |
20 |
50 |
根据表中数据,你认为吸烟与患肺癌有关的把握有
A  B
B  C
C  D
D 
对于散点图下列说法中正确一个是
A通过散点图一定可以看出变量之间的变化规律
B通过散点图一定不可以看出变量之间的变化规律
C通过散点图可以看出正相关与负相关有明显区别
D通过散点图看不出正相关与负相关有什么区别
.右图是2009年中央电视台举办的挑战主持人大赛上,七位评委为某
选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,
所剩数据的平均数和方差分别为( ).
A. , , |
B. , , |
C. , , |
D. , , |

某考察团对全国10个城市进行职工人均工资水平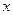 (千元)与居民人均消费水平
(千元)与居民人均消费水平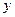 (千元)统计调查,
(千元)统计调查,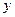 与
与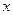 具有相关关系,回归方程为
具有相关关系,回归方程为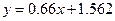 .若某城市居民人均消费水平为7.675(千元),估计该城市人均消费额占人均工资收入的百分比约为( )
.若某城市居民人均消费水平为7.675(千元),估计该城市人均消费额占人均工资收入的百分比约为( )
| A.83% | B.72% | C.67% | D.66% |
右图为甲、乙两运动员在近阶段比赛得分情况的茎叶图.其中 表示甲的得分为( )
表示甲的得分为( )
| A.14,15,11 | B.41,51,11 |
| C.451 | D.10 |
已知变量 具有线性相关关系,测得一组数据如下:
具有线性相关关系,测得一组数据如下: ,
, ,
, ,
, ,
, ,若它们的回归直线方程为
,若它们的回归直线方程为 ,则在这些样本点中任取一点,它在回归直线下方的概率为 ( )
,则在这些样本点中任取一点,它在回归直线下方的概率为 ( )
A. |
B. |
C. |
D. |
两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1的相关指数 为0.86 为0.86 |
B.模型2的相关指数 为0.96 为0.96  |
C.模型3的相关指数 为0.73 为0.73 |
D.模型4的相关指数 为0.66 为0.66 |
下列是x与y之间的一组数据
| X |
0 |
1 |
2 |
3 |
| Y |
1 |
3 |
5 |
7 |
则y关于x的线性回归方程 =
= x+
x+ 对应的直线必过点 ( )
对应的直线必过点 ( )
A.( ,4) ,4) |
B.( ,2) ,2) |
C.(2,2) | D.(1,2) |
若根据10名儿童的年龄 x(岁)和体重 y(㎏)数据用最小二乘法得到用年龄预报体重的回归方程是 y =" 2" x + 7 ,已知这10名儿童的年龄分别是 2、3、3、5、2、6、7、3、4、5,则这10名儿童的平均体重是(***)
| A.17 ㎏ | B.16 ㎏ | C.15 ㎏ | D.14 ㎏ |
右表提供了某厂节能降耗技术改造后生产A产品过程中记录
的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
根据右表提供的数据,求出y关于x的线性回归方程为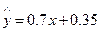 ,那么表中t的值为
,那么表中t的值为
| A.3 | B.3.15 | C.3.5 | D.4.5 |
对于线性相关系数 叙述正确的是( )
叙述正确的是( )
A. ,且 ,且 越大,相关程度越大. 越大,相关程度越大. |
B. ,且 ,且 越大,相关程度越大. 越大,相关程度越大. |
C. ,且 ,且 越大,相关程度越大. 越大,相关程度越大. |
D. ,且 ,且 越大,相关程度越大. 越大,相关程度越大. |