下列命题正确的是( )
| A.单位向量都相等 | B.若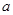 与 与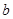 共线, 共线,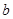 与 与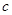 共线,则 共线,则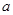 与 与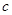 共线 共线 |
C.若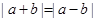 ,则 ,则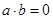 |
D.若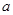 与 与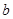 都是单位向量,则 都是单位向量,则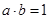 |
关于平面向量
.有下列三个命题:
①若
,则
.②若
,
,则
.
③非零向量
和
满足
,则
与
的夹角为
.
其中真命题的序号为.(写出所有真命题的序号)
在平面向量中有如下定理:设点O,P,Q,R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使 .
.
如图,在ΔABC中,点E为AB边的中点,点F在AC边上,
且CF=2FA,BF交CE于点M,设 ,则
,则
A. |
B. |
C. |
D. |
设是已知平面
上所有向量的集合,对于映射
,记
的象为
.若映射
满足:对所有
、
及任意实数
都有
,则
称为平面
上的线性变换。现有下列命题:
①设是平面
上的线性变换,
、
,则
②若是平面
上的单位向量,对
,设
,则
是平面
上的线性变换;
③对,设
,则
是平面
上的线性变换;
④设是平面
上的线性变换,
,则对任意实数
均有
.
其中的真命题是(写出所有真命题的编号)
在平面向量中有如下定理:设点O,P,Q,R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使 .
.
如图,在ΔABC中,点E为AB边的中点,点F在AC边上,
且CF=2FA,BF交CE于点M,设 ,则
,则 
 ( )
( )
A. |
B. |
C. |
D. |