P为圆A: 上的动点,点
上的动点,点 .线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
.线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
(1)求曲线Γ的方程;
(2)当点P在第一象限,且 时,求点M的坐标.
时,求点M的坐标.
在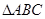 中,角
中,角 的对边分别为
的对边分别为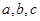 ,且
,且 .
.
(1)求 的值;
的值;
(2)若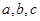 成等差数列,且公差大于0,求
成等差数列,且公差大于0,求 的值.
的值.
P为圆A: 上的动点,点
上的动点,点 .线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
.线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
(1)求曲线Γ的方程;
(2)当点P在第一象限,且 时,求点M的坐标.
时,求点M的坐标.
如图,在斜三棱柱 中,O是AC的中点,
中,O是AC的中点, 平面
平面 ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
各项均为正数的数列 ,
, 满足:
满足: ,
, ,
, ,那么( )
,那么( )
A. |
B. |
C. |
D. |
已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件,今年拟下调销售单价以提高销量,增加收益.据测算,若今年的实际销售单价为x元/件(1≤x≤2),今年新增的年销量(单位:万件)与(2-x)2成正比,比例系数为4.
(1)写出今年商户甲的收益y(单位:万元)与今年的实际销售单价x间的函数关系式;
(2)商户甲今年采取降低单价,提高销量的营销策略是否能获得比往年更大的收益(即比往年收益更多)?说明理由.
在平面直角坐标系xOy中,△ABC的顶点B、C的坐标为B(-2,0),C(2,0),直线AB,AC的斜率乘积为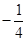 ,设顶点A的轨迹为曲线E.
,设顶点A的轨迹为曲线E.
(1)求曲线E的方程;
(2)设曲线E与y轴负半轴的交点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与曲线E的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,试求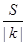 的取值范围.
的取值范围.
已知函数f(x)=ax2-(4a+2)x+4lnx,其中a≥0.
(1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性.
已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件,今年拟下调销售单价以提高销量,增加收益.据测算,若今年的实际销售单价为x元/件(1≤x≤2),今年新增的年销量(单位:万件)与(2-x)2成正比,比例系数为4.
(1)写出今年商户甲的收益y(单位:万元)与今年的实际销售单价x间的函数关系式;
(2)商户甲今年采取降低单价,提高销量的营销策略是否能获得比往年更大的收益(即比往年收益更多)?说明理由.
在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点.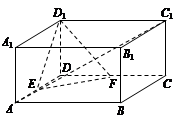
(1)若AC1⊥D1F,求a的值;
(2)若a=2,求二面角E-FD1-D的余弦值.
在平面直角坐标系xOy中,曲线y=x2-2x-3与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若直线x+y+a=0与圆C交于A,B两点,且AB=2,求实数a的值.
如图,已知点D(0,-2),过点D作抛物线 :
: 的切线l,切点A在第二象限。
的切线l,切点A在第二象限。
(1)求切点A的纵坐标;
(2)若离心率为 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k, ,①试用斜率k表示
,①试用斜率k表示 ②当
②当 取得最大值时求此时椭圆的方程。
取得最大值时求此时椭圆的方程。
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量 (升)与行驶速度
(升)与行驶速度 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。
(1)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?