江苏南京市高二第一学期期末调研理科数学试卷
已知a,b∈R,a+bi=(1+2i)(1-i) (i为虚数单位),则a+b的值为 .
记命题p为“若a=b,则cosa=cosb”,则在命题p及其逆命题、否命题、逆否命题中,真命题的个数是 .
在平面直角坐标系xOy中,已知焦点在x轴上的双曲线的渐近线方程为x±2y=0,则该双曲线的离心率为 .
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,ÐBAA1=60°,E为棱C1D1的中点,则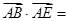 .
.
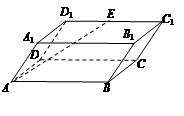
“a=1”是“函数f(x)=x+acosx在区间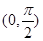 上为增函数”的 条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空).
上为增函数”的 条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空).
在平面直角坐标系xOy中,已知椭圆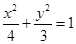 的左焦点为F,直线x-y-1=0,x-y+1=0与椭圆分别相交于点A,B,C,D,则AF+BF+CF+DF= .
的左焦点为F,直线x-y-1=0,x-y+1=0与椭圆分别相交于点A,B,C,D,则AF+BF+CF+DF= .
定义在R上的函数y=f(x)的图像经过坐标原点O,且它的导函数y=f¢(x)的图像是如图所示的一条直线,则y=f(x)的图像一定不经过第 象限.

已知A是曲线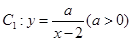 与曲线C2:x2+y2=5的一个公共点.若C1在A处的切线与C2在A处的切线互相垂直,则实数a的值是 .
与曲线C2:x2+y2=5的一个公共点.若C1在A处的切线与C2在A处的切线互相垂直,则实数a的值是 .
已知m∈R,设p:复数z1=(m-1)+(m+3)i (i是虚数单位)在复平面内对应的点在第二象限,q:复数z2=1+(m-2)i的模不超过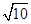 .
.
(1)当p为真命题时,求m的取值范围;
(2)若命题“p且q”为假命题,“p或q”为真命题,求m的取值范围.
在平面直角坐标系xOy中,曲线y=x2-2x-3与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若直线x+y+a=0与圆C交于A,B两点,且AB=2,求实数a的值.
在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点.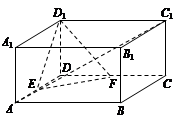
(1)若AC1⊥D1F,求a的值;
(2)若a=2,求二面角E-FD1-D的余弦值.
已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件,今年拟下调销售单价以提高销量,增加收益.据测算,若今年的实际销售单价为x元/件(1≤x≤2),今年新增的年销量(单位:万件)与(2-x)2成正比,比例系数为4.
(1)写出今年商户甲的收益y(单位:万元)与今年的实际销售单价x间的函数关系式;
(2)商户甲今年采取降低单价,提高销量的营销策略是否能获得比往年更大的收益(即比往年收益更多)?说明理由.
已知函数f(x)=ax2-(4a+2)x+4lnx,其中a≥0.
(1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性.
 的导函数为
的导函数为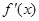 ,则
,则 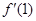 的值为 .
的值为 .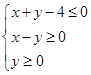 ,则
,则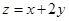 的最大值为 .
的最大值为 .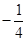 ,设顶点A的轨迹为曲线E.
,设顶点A的轨迹为曲线E.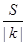 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号