若变量x,y满足约束条件 ,且z=2x+y的最大值和最小值分别为m和n,则m﹣n=( )
,且z=2x+y的最大值和最小值分别为m和n,则m﹣n=( )
| A.5 | B.6 | C.7 | D.8 |
设等差数列 的前n和为Sn,若使得Sn最大,则n等于( )
的前n和为Sn,若使得Sn最大,则n等于( )
| A.7 | B.8 | C.6或7 | D.7或8 |
△ABC的两个顶点为A(﹣1,0),B(1,0),△ABC周长为6,则C点轨迹方程为( )
A. (y≠0) (y≠0) |
B. (y≠0) (y≠0) |
C. (y≠0) (y≠0) |
D.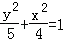 (y≠0) (y≠0) |
设fn(x)是等比数列1,x,x2,…,xn的各项和,则fn(2)等于( )
| A.2n﹣1 | B.2n+1﹣1 | C.2n﹣2 | D.2n+1﹣2 |
在△ABC中,a=15,b=10,A=60°,则cosB=( )
A. |
B. |
C. |
D. |
在如图的电路图中,“开关A的闭合”是“灯泡B亮”的( )

| A.充分非必要条件 |
| B.必要非充分条件 |
| C.充要条件 |
| D.既非充分又非必要条件 |
已知函数f(x)=x2+2x+alnx(a∈R).
(1)当时a=﹣4时,求f(x)的最小值;
(2)若函数f(x)在区间(0,1)上为单调函数,求实数a的取值范围.
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N*,有 2Sn=2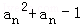 .函数f(x)=x2+x,数列{bn}的首项b1=
.函数f(x)=x2+x,数列{bn}的首项b1=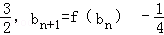 .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令 求证:{cn}是等比数列并求{cn}通项公式;
求证:{cn}是等比数列并求{cn}通项公式;
(Ⅲ)令dn=an•cn,(n为正整数),求数列{dn}的前n项和Tn.
已知数列{an}的前n项和Sn,a1=﹣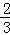 ,Sn+
,Sn+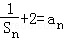 (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn=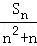 ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣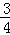 .
.
设函数f(x)=x3+3bx2+3cx有两个极值点x1,x2,且x1∈[﹣1,0],x2∈[1,2],则( )
A.﹣10≤f(x1)≤﹣ |
B.﹣ ≤f(x1)≤0 ≤f(x1)≤0 |
C.0≤f(x1)≤ |
D. ≤f(x1)≤10 ≤f(x1)≤10 |
已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn是数列{an}前n项的和,则 (n∈N+)的最小值为( )
(n∈N+)的最小值为( )
| A.4 | B.3 | C.2 ﹣2 ﹣2 |
D. |