为了满足广大人民群众的消费需求,某商场计划于今年“五一黄金周”期间,用160000元购进一批家电,这批家电的进价和售价如下表:
| 类别 |
彩电 |
冰箱 |
洗衣机 |
| 进价 |
2000 |
1600 |
1000 |
| 售价 |
2200 |
1800 |
1100 |
(1)若全部资金用来购买彩电和洗衣机共100台,问商店可以购买彩电和洗衣机各多少台?
(2)若在现有资金160000元允许的范围内,购买上表中三类家电共100台,其中彩电台数和冰箱台数相同,且购买洗衣机的台数不超过购买彩电的台数,请你算一算有几种进货方案?哪种进货方案能使商店销售完这批家电后获得的利润最大?并求出最大利润.(利润=售价-进价)
已知x +4y-3z = 0,且4x-5y + 2z = 0,x:y:z 为…………( )
| A.1:2:3; | B.1:3:2; | C.2:1:3; | D.3:1:2 |
用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,
则第n个图形黑棋子 枚(用含n的代数式表示,n为自然数)。
下列解方程去分母正确的是 ( )
A.由 ,得2x - 1 =" 3" - 3x; ,得2x - 1 =" 3" - 3x; |
B.由 ,得2(x - 2) - 3x - 2 =" -" 4 ,得2(x - 2) - 3x - 2 =" -" 4 |
C.由 ,得3y + 3 =" 2y" - 3y + 1 - 6y; ,得3y + 3 =" 2y" - 3y + 1 - 6y; |
D.由 ,得12x - 1 =" 5y" + 20 ,得12x - 1 =" 5y" + 20 |
(1)阅读下列材料并填空
例:解方程 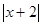 +
+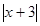 =5
=5
解:① 当x<-3时,x+2<0 ,x+3<0,
所以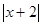 =-x-2,
=-x-2,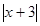 =-x-3
=-x-3
所以原方程可化为 (1) =5
解得 x= (2)
② 当-3≤x <-2时 ,x+2<0 ,x+3≥0,
所以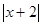 =-x-2,
=-x-2,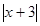 =x+3
=x+3
所以原方程可化为 -x-2+x+3=5
1=5
所以此时原方程无解
③ 当x≥-2时 ,x+2≥0 ,x+3>0,
所以 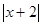 = (3) ,
= (3) ,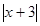 = (4)
= (4)
所以原方程可化为 (5) =5
解得 x= (6)
(2)用上面的解题方法解方程
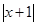 -
-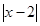 =x-6
=x-6
在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图3),试根据图中的信息,解答下列问题:
(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?说明理由。
 |

(经典题)小刚为书房买灯,现有两种灯可供选购,其中一种是9瓦(即0.009千瓦)的节能灯,售价为49元/盏;另一种是40瓦(即0.04千瓦)的白炽灯,售价为18元/盏.假设两种灯的照明亮度一样,使用寿命都可以达到2800小时,已知小刚家所在地的电价是每千瓦时0.5元.
(1)设照明时间是x小时,请用含x的代数式分别表示用一盏节能灯的费用和用一盏白炽灯的费用(注:费用=灯的售价+电费);
(2)小刚想在这两种灯中选购一盏:
①当照明时间是多少时,使用两种灯的费用一样多;
②试用特殊值判断:
照明时间在什么范围内,选用白炽灯费用低;
照明时间在什么范围内,选用节能灯费用低.
(3)小刚想在这两种灯中选购两盏:假定照明时间是3000小时,使用寿命都是2800小时,请你帮他设计费用最低的选灯方案,并说明理由.