从1、2、3、4、5、6中任取1个数，不大于4的概率是（ ）
A． |
B． |
C． |
D． |
已知M（a，b）是平面直角坐标系xOy中的点，其中a是从l，2，3三个数中任取的一个数，b是从l，2，3，4四个数中任取的一个数．定义“点M（a，b）在直线x+y=n上”为事件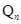
（2≤n≤7，n为整数），则当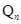的概率最大时，n的所有可能的值为 ．
四张小卡片上分别写有数字1、2、3、4．它们除数字外没有任何区别，现将它们放在盒子里搅匀．
（1）随机地从盒子里抽取一张，求抽到数字2的概率；
（2）随机地从盒子里抽取一张．不放回再抽取第二张．请你用画树状图或列表的方法表示所有等可能的结果，并求抽到的数字之和为5的概率．
已知一个口袋中装有7个只有颜色不同的球，其中3个白球，4个黑球．
（1）求从中随机抽取出一个黑球的概率是多少？
（2）若往口袋中再放入
个白球和
个黑球，从口袋中随机取出一个白球的概率是
，求与之间的函数关系式．
一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字3、4、5、x．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：
解答下列问题：
（1）如果实验继续进行下去，根据上表数据，出现“和为8”的频率将稳定在它的概率附近．估计出现“和为8”的概率是____________．
（2）如果摸出的这两个小球上数字之和为9的概率是
，那么x的值可以取7吗？请用列表法或画树状图法说明理由；如果x的值不可以取7，请写出一个符合要求的x值．
为了了解初三学生参加体育活动的情况，某校对部分初三学生进行了调查，其中一个问题是：“你平均每天参加体育活动的时间是多少？”共有4个选项：
| A．1．5小时以上 | B．1—1．5小时 |
| C．0．5—1小时 | D．0．5小时以下 |
根据调查结果绘制了两幅不完整的统计图如下：
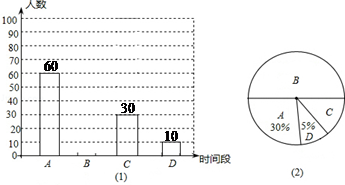
请你根据以上信息解答下列问题：
（1）本次调查的学生人数为 人，图（2）中选项C的圆心角度数为 度，请补全条形统计图。
（2）选择D选项的人中有2人来自一班，2人来自二班，学校准备从这4人中任选两人参加学校组织的师生趣味运动会，请你用列表法或画树状图的方法，求出所选的两人均来自同一个班的概率．
现有5张正面分别标有数字0，1，2，3，4的不透明卡片，它们除数字不同外其余全部
相同。现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为
，则使得关于
的一元二次方程
有实数根，且关于的分式方程
有整数解的概率为 ．
小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查，由调查结果绘制了频数分布直方图，根据图中信息回答下列问题：
（1）求m的值；
（2）从参加课外活动时间在6～10小时的5名学生中随机选取2人，请你用列表或画树状图的方法，求其中至少有1人课外活动时间在8～10小时的概率．
在一个不透明的口袋中装有4个红球和若干个白球，他们除颜色外其他完全相同．通过多次摸球实验后发现，摸到红球的频率稳定在25%附近，则口袋中白球可能有 个．
袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球．下列事件是必然事件的是（ ）
| A．摸出的三个球中至少有一个球是黑球 |
| B．摸出的三个球中至少有一个球是白球 |
| C．摸出的三个球中至少有两个球是黑球 |
| D．摸出的三个球中至少有两个球是白球 |
把一副扑克牌中的三张黑桃牌（它们正面的数字分别为3,4,5）洗匀后正面朝下放在桌面上．小王和小李玩摸牌游戏，游戏规则如下：先由小王随机抽取一张牌，记下牌面数字后放回，洗匀后正面朝下，再由小李随机抽取一张牌，记下牌面数字．当两张牌的牌面数字相同时，小王赢；当两张牌的牌面数字不同时，小李赢．
（1）请利用画树状图或列表的方法表示出所有可能出现的结果；
（2）分析游戏规则对双方是否公平，并说明理由．
在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其他完全相同，小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在15%和45%，则口袋中白色球的个数可能是_________________个．
粤公网安备 44130202000953号