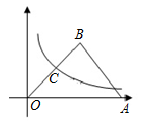
如图,等边三角形OAB的一边OA在x轴上,双曲线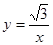
 在第一象限内的图像经过OB边的中点C,则点B的坐标是( )
在第一象限内的图像经过OB边的中点C,则点B的坐标是( )
A.( 1,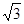 ) ) |
B.(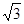 ,1 ) ,1 ) |
C.( 2,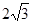 ) ) |
D.(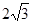 ,2 ) ,2 ) |
如图,在平面直角坐标系xOy中,△ABC的边AC在x轴上,边BC⊥x轴,双曲线y=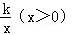 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).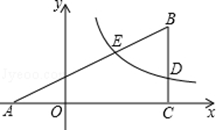
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC=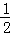 ,求k的值和点B的坐标.
,求k的值和点B的坐标.
如图,将一块直角三角板OAB放在平面直角坐标系中,B(1,0),∠OAB=30°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线 ,以直线
,以直线 为对称轴,线段OB经轴对称变换后的像是O′B′.
为对称轴,线段OB经轴对称变换后的像是O′B′.

(1)当点O′与点A重合时,点P的坐标是 .
(2)设P(t,0)当O′B′与双曲线有交点时,t的取值范围是 .
如图,已知点A的坐标( ,3),AB⊥x轴,垂足为B,连接OA,反比例函数y=
,3),AB⊥x轴,垂足为B,连接OA,反比例函数y= (k>0)的图象与线段OA、AB分别交于C、D两点,若AB=3BD.以C点为圆心,2CA长为半径作圆C.
(k>0)的图象与线段OA、AB分别交于C、D两点,若AB=3BD.以C点为圆心,2CA长为半径作圆C.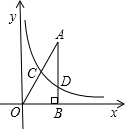
(1)求k的值;
(2)求点C坐标;
(3)判断⊙C与x轴的位置关系.
已知A(-1,y1);B(2,y2);C(3,y3)在反比例函数 的图象上,则下列结论中正确的是( )
的图象上,则下列结论中正确的是( )
| A.y1>y2>y3 | B.y1>y3>y2 | C.y3>y1>y2 | D.y2>y3>y1 |
如果反比例函数 与一次函数y=mx-4(m≠0)的图象都经过点A(a,2).
与一次函数y=mx-4(m≠0)的图象都经过点A(a,2).
(1)求点A的坐标及m的值;
(2)求另一个交点B的坐标.
已知A(-4,y1),B(-3,y2),C(3,y3)三点都在反比例函数y=-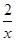 的图象上,则y1,y2,y3的大小关系为 .(用“<”连接)
的图象上,则y1,y2,y3的大小关系为 .(用“<”连接)
如图,双曲线y= 与矩形OABC的对角线OB相交于点D,且DB:OD=2:3,则矩形OABC的面积为( )
与矩形OABC的对角线OB相交于点D,且DB:OD=2:3,则矩形OABC的面积为( )

A. |
B. |
C. |
D.8 |
三张完全相同的卡片上分别写有函数 ,
, ,
, ,从中随机抽取一张,则所得卡片上函数的图象在第一象限内
,从中随机抽取一张,则所得卡片上函数的图象在第一象限内 随
随 的增大而增大的概率是 .
的增大而增大的概率是 .
下列图形中,阴影部分的面积相等的是( )

| A.①② | B.②③ | C.③④ | D.①④ |