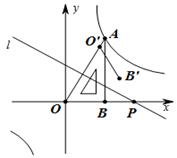
如图，将一块直角三角板OAB放在平面直角坐标系中，B（1，0），∠OAB＝30°，点A在第一象限，过点A的双曲线为y= ，在x轴上取一点P，过点P作直线OA的垂线
，以直线为对称轴，线段OB经轴对称变换后的像是O′B′．
（1）当点O′与点A重合时，点P的坐标是 ．
（2）设P（t，0）当O′B′与双曲线有交点时，t的取值范围是 ．
是方程
的根，则
_________＿
＿．
，那么
.
.相关知识点
推荐套卷
如图，将一块直角三角板OAB放在平面直角坐标系中，B（1，0），∠OAB＝30°，点A在第一象限，过点A的双曲线为y= ，在x轴上取一点P，过点P作直线OA的垂线，以直线为对称轴，线段OB经轴对称变换后的像是O′B′．
（1）当点O′与点A重合时，点P的坐标是 ．
（2）设P（t，0）当O′B′与双曲线有交点时，t的取值范围是 ．
粤公网安备 44130202000953号