初中数学菱形的性质试题

如图，若菱形 ABCD的顶点 A， B的坐标分别为（3，0），（﹣2，0），点 D在 y轴上，则点 C的坐标是 　　．

如图，在边长为3的菱形 ABCD中，∠ A＝60°， M是 AD边上的一点，且 AM＝ $\frac{1}{3}$ AD， N是 AB边上的一动点，将△ AMN沿 MN所在直线翻折得到△ A′ MN，连接 A′ C．则 A′ C长度的最小值是 　　．

一个菱形的边长是方程 x ²﹣8 x+15＝0的一个根，其中一条对角线长为8，则该菱形的面积为（　　）

A．

48

B．

24

C．

24或40

D．

48或80

已知菱形的边长为3，较短的一条对角线的长为2，则该菱形较长的一条对角线的长为（　　）

A．

2 $\sqrt{2}$

B．

2 $\sqrt{5}$

C．

4 $\sqrt{2}$

D．

2 $\sqrt{10}$

（1）【探究发现】

如图1，∠ EOF的顶点 O在正方形 ABCD两条对角线的交点处，∠ EOF＝90°，将∠ EOF绕点 O旋转，旋转过程中，∠ EOF的两边分别与正方形 ABCD的边 BC和 CD交于点 E和点 F（点 F与点 C， D不重合）．则 CE， CF， BC之间满足的数量关系是 　 　．

（2）【类比应用】

如图2，若将（1）中的"正方形 ABCD"改为"∠ BCD＝120°的菱形 ABCD"，其他条件不变，当∠ EOF＝60°时，上述结论是否仍然成立？若成立，请给出证明；若不成立，请猜想结论并说明理由．

（3）【拓展延伸】

如图3，∠ BOD＝120°， OD＝ $\frac{3}{4}$ ， OB＝4， OA平分∠ BOD， AB＝ $\sqrt{13}$ ，且 OB＞2 OA，点 C是 OB上一点，∠ CAD＝60°，求 OC的长．

如图，矩形 ABCD与菱形 EFGH的对角线均交于点 O，且 EG∥ BC，将矩形折叠，使点 C与点 O重合，折痕 MN过点 G．若 AB＝ $\sqrt{6}$ ， EF＝2，∠ H＝120°，则 DN的长为（　　）

A．

$\sqrt{6}$ - $\sqrt{3}$

B．

$\frac{\sqrt{6}+\sqrt{3}}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

2 $\sqrt{3}-\sqrt{6}$

如图，菱形 ABCD周长为20，对角线 AC、 BD相交于点 O， E是 CD的中点，则 OE的长是（　　）

A．

2.5

B．

3

C．

4

D．

5

如图，已知 A、 F、 C、 D四点在同一条直线上， AF＝ CD， AB∥ DE，且 AB＝ DE．

（1）求证：△ ABC≌△ DEF；

（2）若 EF＝3， DE＝4，∠ DEF＝90°，请直接写出使四边形 EFBC为菱形时 AF的长度．

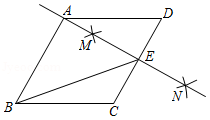
如图，在菱形 ABCD中，按以下步骤作图：

①分别以点 C和点 D为圆心，大于 $\frac{1}{2}$ CD为半径作弧，两弧交于点 M， N；

②作直线 MN，且 MN恰好经过点 A，与 CD交于点 E，连接 BE，

则下列说法错误的是（　　）

A．	∠ABC＝60°	B．	S △ ABE＝2S △ ADE
C．	若AB＝4，则BE＝ $4\sqrt{7}$	D．	sin∠CBE＝ $\frac{\sqrt{21}}{14}$

如图，菱形 ABCD的面积为120 cm ²，正方形 AECF的面积为72 cm ²，则菱形的边长为 　　．（结果中如有根号保留根号）

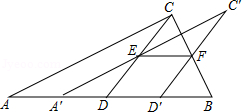
如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD沿DB方向平移到△A′C′D′的位置，若平移开始后点D′未到达点B时，A′C′交CD于E，D′C′交CB于点F，连接EF，当四边形EDD′F为菱形时，试探究△A′DE的形状，并判断△A′DE与△EFC′是否全等？请说明理由．

如图，菱形ABCD的边AB＝8，∠B＝60°，P是AB上一点，BP＝3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点A′．当CA′的长度最小时，CQ的长为（　　）

A．5B．7C．8D． $\frac{13}{2}$

如图，将边长为4的菱形 ABCD纸片折叠，使点 A恰好落在对角线的交点 O处，若折痕 EF＝2 $\sqrt{3}$ ，则∠ A＝（　　）

A．

120°

B．

100°

C．

60°

D．

30°

如图，菱形 ABCD的边长为2 cm，∠ A＝120°，点 E是 BC边上的动点，点 P是对角线 BD上的动点，若使 PC+ PE的值最小，则这个最小值为 　　．

如图，菱形 ABCD的边长为2，∠ ABC＝60°，过点 D作 DE∥ AC， DE＝ $\frac{1}{2}$ AC，连接 AE，则△ ADE的周长为 　 　．