如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第n个图案中有2017个白色纸片,则n的值为( )

A.671B.672C.673D.674
如图,由一些点组成形如正多边形的图案,按照这样的规律摆下去,则第 n( n>0)个图案需要点的个数是 .

将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n= .

如图,已知直线 ,分别过
,分别过 轴上的点
轴上的点 、
、 、
、 、
、 ,作垂直于
,作垂直于 轴的直线交
轴的直线交 于点
于点 、
、 、
、 、
、 ,将△
,将△ ,四边形
,四边形 、
、 、四边形
、四边形 的面积依次记为
的面积依次记为 、
、 、
、 、
、 ,则
,则


A. B.
B. C.
C. D.
D.
如图 ,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为
,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为 ,
, ,
, ,
, ,
,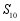 ,则
,则 .
.

如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1,边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2,以A2F2为边作正六边形A2B2C2D2E2F2,边C2D2所在的直线分别交OM、ON于点A3、F3,再以A3F3为边作正六边形A3B3C3D3E3F3,…,依此规律,经第n次作图后,点Bn到ON的距离是 .

一个电子跳蚤在数轴上做跳跃运动.第一次从原点 起跳,落点为 ,点 表示的数为1;第二次从点 起跳,落点为 的中点 ,第三次从 点起跳,落点为 的中点 ;如此跳跃下去 最后落点为 的中点 ,则点 表示的数为 .

如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形 ,按这样的方法拼成的第 个正方形比第 个正方形多 个小正方形.

如图,四边形 是边长为1的正方形,以对角线 为边作第二个正方形 ,连接 ,得到△ ;再以对角线 为边作第三个正方形 ,连接 ,得到△ ,再以对角线 为边作第四个正方形 ,连接 ,得到△ , ,设△ ,△ ,△ , ,的面积分别为 , , , ,如此下去,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
1010 |
一个电子跳蚤在数轴上做跳跃运动.第一次从原点 起跳,落点为 ,点 表示的数为1;第二次从点 起跳,落点为 的中点 ,第三次从 点起跳,落点为 的中点 ;如此跳跃下去 最后落点为 的中点 ,则点 表示的数为 .

如图, ,正方形 ,正方形 ,正方形 ,正方形 , ,的顶点 , , , , ,在射线 上,顶点 , , , , , ,在射线 上,连接 交 于点 ,连接 交 于点 ,连接 交 于点 , ,连接 交 于点 ,连接 交 于点 , ,按照这个规律进行下去,设 与△ 的面积之和为 ,△ 与△ 的面积之和为 ,△ 与△ 的面积之和为 , ,若 ,则 等于 .(用含有正整数 的式子表示)

如图, ,点 在射线 上,且 ,过点 作 交射线 于点 ,在射线 上截取 ,使得 ;过点 作 交射线 于点 ,在射线 上截取 ,使得 ; ;按照此规律进行下去,则 长为 .
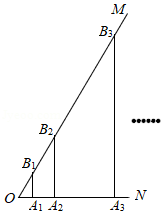
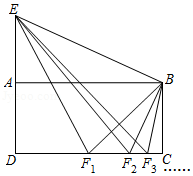
如图,四边形 是矩形,延长 到点 ,使 ,连接 ,点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ; ;按照此规律继续进行下去,若矩形 的面积等于2,则△ 的面积为 .(用含正整数 的式子表示)