高中物理磁感应强度试题

如图10所示，正方形线框ABCD的总电阻R为0.4Ω，质量m为0.1kg，边长为0.4m，两虚线之间是垂直于线框平面向里的匀强磁场，磁场上限（上面一条虚线）正好过AC和BD的中点，磁感应强度从2T开始以5T／s的变化率均匀增大，当磁感应强度为多大时，悬线的拉力为零？（AB边水平）

把一根长l = 10cm的导线垂直磁感线方向放入如图所示的匀强磁场中，

（1）当导线中通以I₁ = 2A的电流时，导线受到的安培力大小为1.0×10^－7N，则该磁场的磁感应强度为多少？
（2）若该导线中通以I₂ = 3A的电流，则此时导线所受安培力大小是多少？方向如何？

（1）求小球从抛出点至第一落地点P的水平位移S 的大小；
（2）若在空间竖直方向加一个匀强电场，发现小球水平抛出后做匀速直线运动，求该匀强电场的场强E的大小和方向；
（3）若在第（2）基础上再加一个垂直纸面向外的匀强磁场，发现小球抛出后沿圆弧轨迹运动，第一落地点仍然是P点，求该磁场的磁感应强度B的大小。

所示为一块霍尔元件，其横载面为矩形，霍尔元件的长、宽、高分别为c、b、d。已知其单位体积内的电子数为n、电子电荷量e.将此元件放在匀强磁场中，磁场方向沿Z轴方向，并通有沿x轴方向的电流I。
试证明在磁感应强度为定值B时，稳定后此元件的两个侧面的电势差

水平面上两根足够长的金属导轨平行固定放置，间距为L，一端通过导线与阻值为R的电阻连接；导轨上放一质量为m的金属杆（如图1（a）所示），金属杆与导轨的电阻忽略不计。均匀磁场竖直向下，用与导轨平行的恒定拉力F作用在金属杆上，杆最终将做匀速运动。当改变拉力的大小时，相对应的匀速运动速度v也会变化，v和F的关系如图1（b）所示（取重力加速度）:
（1）若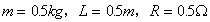；则磁感应强度B为多大？
（2）由图线的截距可求得什么物理量？其值为多少？

如图所示，图的右侧MN为一竖直放置的荧光屏，O为它的中点OO′与荧光屏垂直，且距离为L，在MN的左侧空间存在着方向水平向里的匀强电场，场强大小为E.乙图是从左边去看荧光屏得到的平面图，在荧光屏上以O为原点建立如图的直角坐标系.一束质量为m、电量为+q的带电粒子以相同的初速度v₀从O′点沿O′O方向射入电场区域.粒子的重力和粒子间的相互作用都可忽略不计.
（1）若再在MN左侧空间加一个匀强磁场，使得荧光屏上的亮点恰好位于原点O处，求这个磁场的磁感应强度B的大小和方向
（2）如果磁感应强度B的大小保持不变，方向变为与电场方向相同，则荧光屏上的亮点位于图中A点处，已知A点的纵坐标为y=，求A点横坐标的数值.

在赤道附近的地磁场可看做是沿南北方向的匀强磁场，磁感应强度的大小是0.5×10^－4T。如果赤道上有一根沿东西方向的直导线，长20m，通有从东向西的电流30A，问地磁场对这根导线的作用力有多大？方向如何？

在倾角为α的光滑斜面上，放置一个通有电流为I、长为L、质量为m的导体棒，如图所示，求：
（1）欲使棒静止在斜面上，外加匀强磁场的磁感应强度B的最小值和方向。
（2）欲使棒静止在斜面上且对斜面无压力，外加匀强磁场的磁感应强度B的大小和方向

（1）判断电场的方向及物体带正电还是带负电； 
（2）求磁感应强度B的大小；
（3）求物体与挡板碰撞过程中损失的机械能。

一根长为L的金属棒，在匀强磁场中沿垂直于磁场方向做匀速运动，金属棒与磁感线垂直，棒中产生的感应电动势为e，经时间t，金属棒运动了位移为s，则此时磁场的磁感应强度的大小应为（   ）

A．

B．

C．

D．

通有方向如图所示电流I 的螺线管内外空间中，放有a、b、c三个小磁针，当三个小磁针静止时[　　]

A．a、b、c左端都为N极

B．b、c左端为N极，a右端为N极

C．a、c右端为N极，b左端为N极

D．a、b左端为N极，c右端为N极

在磁感应强度为，竖直向上的匀强磁场中，放置一根长通电直导线，电流的方向垂直纸面向外，如图所示，a、b、c、d是以直导线为圆心的同一圆周上的四点，在这四点中[    ]

A．c、d两点的磁感应强度大小相等

B．a、b两点的磁感应强度大小相等

C．a点的磁感应强度的值最小

D．b点的磁感应强度的值最大

下面关于磁场的一些说法中正确的是[　　]

A．所有的磁场都是由于电荷的运动而产生的，即都是由电流产生的

B．所有的磁场的磁感线都是闭合曲线，或者伸向无穷远

C．磁场中某点的磁感线的切线方向就是磁感应强度的方向，即小磁针N极在该点的受力方向

D．某小段通电导线不受磁场力的作用，说明该点的磁感应强度为零

 

（1）磁感应强度B的大小；
（2）在0～0.5s时间内金属棒的加速度a的大小；
（3）若在0～0.3s时间内电阻R产生的热量为0.15J，则在这段时间内电动机做的功。