高中物理磁感应强度试题

如图所示，真空中有中间开有小孔的两平行金属板竖直放置构成电容器，给电容器充电使其两极板间的电势差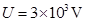，以电容器右板小孔所在位置为坐标原点建立图示直角坐标系xoy。第一象限内有垂直纸面向里的匀强磁场，磁场的上边界MN平行于x轴，现将一质量、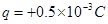且重力不计的带电粒子从电容器的左板小孔由静止释放，经电场加速后从右板小孔射出磁场，该粒子能经过磁场中的P点，P点纵坐标为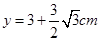。若保持电容器的电荷量不变，移动左板使两板间距离变为原来的四分之一，调整磁场上边界MN的位置，粒子仍从左板小孔无初速度释放，还能通过P点，且速度方向沿y轴正向。求磁场的磁感应强度B？

如图所示，在直角坐标系中，第二象限有一水平放置的平行板电容器，两板间距离为d，下极板与x轴重合，板间有图示方向的匀强磁场，磁感应强度为B，一带电粒子（不计重力）沿两板间中线射入并沿中线进入第一象限，若在第一象限只存在与y轴平行的匀强电场时，粒子刚好通过x轴上的M点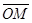（=d），若在第一象限只存在垂直于纸面的匀强磁场时，粒子也刚好通过M点，已知该电场强度和磁感应强度的比值为k，求：平行板电容器两极板间的电压为多少？

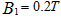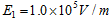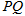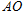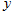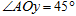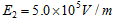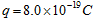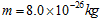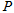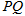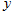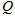如图所示的平行板之间，存在着相互垂直的匀强磁场和匀强电场，磁场的磁感应强度，方向垂直纸面向里，电场强度，为板间中线．紧靠平行板右侧边缘坐标系的第一象限内，有一边界线，与轴的夹角，边界线的上方有垂直纸面向外的匀强磁场，磁感应强度，边界线的下方有水平向右的匀强电场，电场强度，在x轴上固定一水平的荧光屏．一束带电荷量、质量的正离子从点射入平行板间，沿中线做直线运动，穿出平行板后从轴上坐标为的点垂直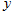轴射入磁场区，最后打到水平的荧光屏上的位置．求：（不计离子的重力影响）

（1）离子在平行板间运动的速度大小．
（2）离子打到荧光屏上的位置的坐标．
（3）现只改变区域内磁场的磁感应强度大小，使离子都不能打到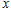轴上，磁感应强度大小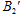应满足什么条件？

如图所示为一种自动跳闸的闸刀开关，O是转动轴，A是绝缘手柄，C是闸刀卡口，M、N接电源线，闸刀处于垂直纸面向里，B=1T的匀强磁场中，CO 间距离为10cm，当磁场力为0.2 N时，闸刀开关会自动跳开。则要使闸刀开关能跳开，CO中通过的电流的大小和方向为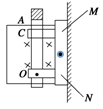

A．电流方向C→O	B．电流方向O→C
C．电流大小为1A	D．电流大小为0.5A

(18分)一个质量为m，带电量为q（负电）的小球（可看成质点）从坐标原点O以沿x轴负方向的速度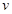₀开始运动，在第一象限存在水平向右的匀强电场，场强大小E₁=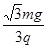。第二象限存在竖直向下的匀强电场，大小E₂=，和垂直纸面向里的长方形有界磁场，磁感应强度为B（图中未画出），坐标原点O在磁场中，小球通过y轴上的M点进入第一象限恰好做减速直线运动（重力加速度g，电场区域足够大）。O、M两点距离为L。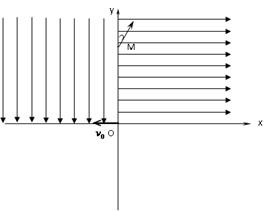

求：（1）=？
（2）长方形区域磁场的最小面积，
（3）小球从坐标原点出发到速度减到零所需时间。

如图所示，在xOy平面内，以O₁(0,R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B₁，x轴下方有一直线ab，ab与x轴相距为d，x轴与直线ab间区域有平行于y轴的匀强电场E，在ab的下方有一平行于x轴的感光板MN，ab与MN间区域有垂直于纸平面向外的匀强磁场B₂。在0≤y≤2R的区域内，质量为m、电荷量为e的电子从任何位置从圆形区域的左侧沿x轴正方向以速度v₀射入圆形区域，经过磁场B₁偏转后都经过O点，然后进入x轴下方。已知x轴与直线ab间匀强电场场强大小，ab与MN间磁场磁感应强度。不计电子重力。

（1）求圆形区域内磁场磁感应强度B₁的大小？
（2）若要求从所有不同位置出发的电子都不能打在感光板MN上，MN与ab板间的最小距离h₁是多大？
（3）若要求从所有不同位置出发的电子都能打在感光板MN上，MN与ab板间的最大距离h₂是多大？当MN与ab板间的距离最大时，电子从O点到MN板，运动时间最长是多少？

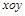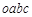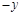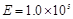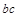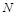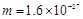在如图所示的直角坐标系中，矩形区域内有垂直于纸面向外的匀强磁场，磁感应强度大小为B=5.0×10^-2T；第一象限内有沿方向的匀强电场，电场强度大小为N/C。已知矩形区域边长为0.06m，ab边长为0.20m。在边中点处有一放射源，某时刻，放射源沿纸面向磁场中各方向均匀地辐射出速率均为m/s的某种带正电粒子，带电粒子质量kg，电荷量kg，不计粒子重力，求：(计算结果保留两位有效数字)

(1)粒子在磁场中运动的半径；
(2)从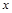轴上射出的粒子中，在磁场中运动的最短路程为多少?
(3)放射源沿-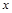方向射出的粒子，从射出到从轴离开所用的时间。